skip to main |
skip to sidebar
Queridos lectores y amigos,
Este blog de física se acaba aquí. La vida trae retos nuevos y hay cambios que afrontar. Gracias por las lecturas y los comentarios.
This blog is finished. Life brings new challenges and there are new situations to be faced. Thanks for reading and commenting.
Un saludo cordial,
Juanjo
En los libros de texto modernos el campo gravitatorio o a veces también la fuerza gravitatoria se idenfitica con la curvatura del espacio-tiempo. Esto es, ahí donde el espacio difiere de uno plano, donde el espacio-tiempo adquiere curvatura, ahí existe un campo gravitatorio actuando. No obstante, esta no era por ejemplo la posición de Einstein. Einstein identificaba la gravitación con los símbolos de Christoffel, en definitiva, con aceleraciones. Einstein tomaba su principio de equivalencia al pie de la letra y asumía que gravitación y aceleraciones no son sólo equivalentes en cierto sentido, sino que son estríctamente lo mismo.
El principio de equivalencia en la formulación original de Einstein
Un observador que está cayendo desde el tejado de su casa no experimenta campo gravitatorio, al menos en sus inmediaciones. Este cruel experimento mental es lo que Albert Einstein denominó "der glückischste Gedanke meines Lebens" (la idea más feliz de mi vida), y sintetiza básicamente la esencia de la relatividad general (un interesante artículo sobre la historia de la relatividad general en astroseti Historia de la Teoría General de la Relatividad), en concreto el principio de equivalencia.
El principio de equivalencia nos dice que en caída libre el campo gravitatorio no existe y que los observadores en caída libre pueden considerarse, por tanto, como observadores inerciales, es decir, libres de cualquier fuerza que actúa sobre ellos. Impedir la caída de uno de estos observadores, por ejemplo por medio de una superficie que lo sostenga y lo deje en reposo, equivale a someterlo a una aceleración uniforme. En la superficie de la tierra es lo mismo considerar que estamos en un campo gravitatorio uniforme que apunta hacia abajo, que considerar que estamos en un sistema acelerado hacia arriba y medimos con ello una fuerza inercial (ficticia) hacia abajo. La gravitación es con ello una fuerza ficticia, y de hecho es esto lo que permite eliminar a la gravitación de forma local con un cambio de coordenadas. En definitiva, para un observador en reposo el efecto del campo gravitatorio uniforme y el de una aceleración uniforme son equivalentes. Existe por tanto una equivalencia entre ambas descripciones.
La definición de campo gravitatorio en la formulación de Einstein y la moderna
Según esta definición de Einstein, el campo gravitatorio es todo aquello que actúa de forma universal desviando a las partículas de trayectorias rectas y velocidad uniforme, acelerándolas, es decir, cambiando 
, que es la forma de la ecuación geodésica cuando los símbolos de Christoffel son cero. Esta ecuación geodésica en la relatividad general se generaliza a ( dx^{\sigma} / dt ) = 0)
para t un tiempo propio a lo largo de la geodésica. Las dos ecuaciones son equivalentes cuando 
, es decir, los símbolos de Christoffel son cero. Según la definición de Einstein el campo gravitatorio son los 
. Aquí un par de citas de Einstein sobre el tema ("The Foundation of the General Theory of Relativity" de 1916):
It will be seen from these reflections that in pursuing the general theory of relativity we shall be led to a theory of gravitation, since we are able to “produce” a gravitational field merely by changing the system of coordinates.
If the vanish, then the point moves uniformly in a straight line. These quantities therefore condition the deviation of the motion from uniformity. They are the components of the gravitational field.
Los símbolos de Christoffel pueden hacerse cero con un cambio de coordenadas, pero la curvatura no ya que es invariante (el escalar de curvatura por ejemplo). El ejemplo más sencillo que soporta la interpretación de Einstein es el campo gravitatorio uniforme. Un campo gravitatorio uniforme es un campo gravitatorio, pero su curvatura es nula. No obstante, se habla de "campo gravitatorio", y, en un sistema de coordenadas apropiado, existe una aceleración, resultado de símbolos de Christofell no nulos, que se identifica con la fuerza de la gravedad. En ese sentido la "fuerza de la gravedad" es algo dependiente del observador. Todo acorde con su formulación del principio de equivalencia.
En la interpretación moderna de la gravitación el término "campo gravitatorio" se suele reservar sin embargo para la curvatura del espacio-tiempo. Independientemente de terminologías en la relatividad general lo que hay es una geometría del espacio-tiempo, descrita por el tensor de Einstein 
acoplada a un momento y energía de la materia, descrita por el tensor de energía momento 
. En concreto, se trata de las ecuaciones de Einstein: 
. Desde el punto de vista de la discusión terminológica mencionada aquí se pueden distinguir varios casos:
- Espacio-tiempo con curvatura. En la terminología moderna tan pronto existe curvatura (generada, en general, por un tensor de energía-momento) se habla de campo gravitatorio. El problema terminológico aparece cuando no hay curvatura.
- Espacio-tiempo sin curvatura y sin energía-momento. Este es el caso del campo gravitatorio uniforme, con aceleraciones no nulas resultado de un cambios de coordenadas en un espacio-tiempo plano.
- Espacio-tiempo sin curvatura y con energía-momento. Estas suelen ser soluciones que violan alguna condición energética, pero en principio posibles. Concrétamente por ejemplo una "cuerda cósmica" o una "pared cósmica". El espacio-tiempo creado por una cuerda cósmica es plano globalmente, pero no es topológicamente equivalente al espacio-tiempo plano de Minkowski. Este espacio-tiempo puede imaginarse de la siguiente forma: una circunferencia concéntrica a la cuerda en una sección perpendicular a ella no mide 2 pi r, sino menos, ya que al espacio-tiempo le falta un sector angular (es un espacio-tiempo cónico). En estos casos no hay campo gravitatorio con la terminología moderna ni con la de Einstein. No obstante, está claro que algo pasa ahí, algo producido por un contenido material, dando lugar a algo diferente al espacio-tiempo plano.
El concepto de campo gravitatorio de Einstein provenía de ajustarse a su formulación del principio de equivalencia. En la forma moderna de la teoría el concepto de campo gravitatorio es diferente, como hemos visto. Más allá de definiciones arbitrarias la verdad, desde el punto de vista de la teoría, está en las ecuaciones de Einstein. Como hemos visto, tampoco el concepto moderno de campo gravitatorio tampoco captura completamente la esencia de la gravitación que nos es dada en las ecuaciones de Einstein. En principio de equivalencia, por su lado, ha sido reformulado a tres versiones diferentes, el principio débil, el de Einstein y el fuerte. Su relación con las ideas originales de Einstein y las relaciones entre estas tres versiones nos ocuparán en otro artículo.
La noción de observables parciales y completos, dependientes e independientes, viene definida en el artículo Partial Observables de Carlo Rovelli, http://arxiv.org/abs/gr-qc/0110035. Para entenderla lo mejor es un ejemplo mencionado en el artículo mismo. Imaginemos un conjunto de cartas. Cada una de ellas tiene escrito un número natural N en una de sus caras y un número natural n en la otra cara. Leemos una carta tras la otra y observamos que siempre existe una correlación entre N y n, es decir, N es una función de n, N = N(n). Por ejemplo: si n menor que 5, entonces N = 0, si n mayor o igual que 5, entonces N = 1.
Según las definiciones de arriba, n y N, por separado, son observables parciales. Podemos leerlos pero no podemos predecirlos por separado. No obstante, N(n) es un observable completo. Los pares (N, n) podemos leerlos pero además predecirlos, en el sentido que sabemos que si n toma un determinado valor, como por ejemplo 7, entonces N valdrá N(7) = 1. Si la correlación entre observables parciales n y N se puede expresar como la función de N respecto de n, pero no de n respecto de N, como es el caso en el ejemplo, entonces n es un observable independiente, mientras que N es un observable dependiente.
En la teoría cuántica de campos los observables parciales son las posiciones y tiempos, así como los valores del campo. No obstante, hay una diferencia entre ambos, ya que mientras los valores del campo son observables dependientes, las posiciones y los tiempos son observables independientes. Finalmente el valor del campo para una posición y un tiempo determinado es un observable completo. Lo importante de notar es que esto refiere a la teoría cuántica de campos que, de alguna forma, representa nuestra intuición de lo que es espacio y tiempo absolutos y estáticos sobre los cuales los campos actúan. No obstante, en la relatividad general no existen observables independientes. Esto es así porque el espacio y el tiempo, y en definitiva el campo gravitatorio, no deben tener una preferencia conceptual frente a los demás campos.
Sin duda el campo gravitatorio es algo especial debido a su universalidad. Es precisamente la universalidad del campo gravitatorio, su efecto sobre todo ente físico, lo que nos lleva a identificar espacio y tiempo como observables parciales independientes en la teoría cuántica de campos: posiciones y tiempos son algo identificable de forma independiente ya que el espacio-tiempo es considerado un escenario donde el resto de las interacciones tienen lugar. No obstante, en la relatividad general su universalidad no lo convierte en un escenario predefinido sino que su existencia y sus propiedades están en relación a la existencia y propiedades de la materia, como muestra el famoso argumento del agujero de Albert Einstein.
Una manera formal de hablar sobre el argumento del agujero es tratando con el concepto de difeomorfismos. Los difeomorfismos son transformaciones de coordenadas activas, mientras que las meras transformaciones de coordenadas son pasivas. La mera transformación de coordenadas deja el espacio-tiempo intacto y mueve las coordenadas, mientras que el difeomorfismo mueve todos los campos del espacio-tiempo y deja las coordenadas intactas. Mientras que una transformación de coordenadas nunca puede dar lugar a una simetría dinámica de una acción los difeomorfismos sí pueden y esa es la diferencia principal. La idea de difeomorfismos captura bien esa eliminación del escenario absoluto, cualquier campo es relativo al otro y la noción de puntos del espacio-tiempo carece de valor absoluto.
Estríctamente la noción de difeomorfismo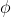 
como mapa entre dos variedades 
se aplica sobre todas las variables dinámicas de una acción. Las coordenadas no son variables dinámicas por lo que, intuitivamente, su transformación ha de ser deshecha de forma que sean evaluadas en la variedad original. Formalmente la mejor forma de entender esto es la noción de derivada de Lie 
a lo largo de un campo vectorial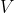 
. Se define como:
El primer término representa la transformación de la variedad a lo largo de las curvas integrales de un campo vectorial:
Esto significa que todos las variables dinámicas en el espacio-tiempo son movidas a lo largo de las flechas adquiriendo un valor nuevo. El segundo término de la expresión de la derivada de Lie es una transformación de coordenadas de los valores nuevos dados por el campo vectorial que define la transformación a los valores antiguos. Por tanto, una acción es invariante frente a difeomorfismos si y sólo si la derivada de Lie de todas las variables dinámicas o todos los campos tensoriales que aparecen en ella es cero. Y esto es precisamente lo que ocurre en la acción de Einstein-Hilbert de la relatividad general, y, en general cualquier acción escrita en forma covariante.
Detalles matemáticos en: Symmetry Transformations, the Einstein-Hilbert Action, and Gauge Invariance, E. Bertschinger.
El problema de la entropía del universo y sus condiciones iniciales es uno que levanta mucho polvo y trae una larga lista de literatura. El siguiente artículo lo trata desde dos perspectivas que están sacadas de las referencias citadas al final - un artículo publicado y una entrada de blog. En concreto, Sean Carroll, cosmólogo, defendiendo su planteamiento del problema, el clásico en gran parte de la literatura, y Lubos Motl, físico teórico, proporcionando una visión muy consistente en mi parecer sobre el problema en cuestión y que en definitiva viene a negarlo como tal.
El problema de las condiciones iniciales
Las ecuaciones diferenciales de la física nos permiten obtener soluciones que resuelven la evolución temporal del universo a partir de ciertas condiciones en un instante determinado. Esto es, dado por ejemplo el estado de nuestro universo en el momento presente y dadas esas leyes dinámicas, se puede, en principio, resolver toda su historia, y dar por ejemplo con el estado en el instante de la singularidad inicial hace 13.7 mil millones de años. De igual forma, dadas las condiciones iniciales en la singularidad inicial y dadas esas leyes se puede explicar o dar con el estado del universo en el presente.
En un problema de valores iniciales es precisamente esto lo que se quiere: encontrar o predecir un estado futuro a partir de ciertas condiciones iniciales dadas. Pero ¿cuáles han de ser estas condiciones iniciales? ¿Por qué deberíamos decirle al nuestro universo que observamos hoy cómo empezar a ser o a expandir? Nihil est sine ratione: cualquier elección injustificada convierte las condiciones en indemostrables y no ducibles, elevándolas al mismo estatus conceptual que los mismos principios y leyes de la teoría.
En concreto, lo que nos gustaría es dar con unas condiciones iniciales de nuestro universo las cuales podemos calificar de naturales en cierto modo. El concepto de naturalidad en este contexto es algo vago, pero en ciertos casos simples lo vemos claramente relacionado con las leyes conocidas. Por ejemplo, la homogeneidad y la isotropía en la distribución de materia es un estado inestable frente al colapso gravitacional siempre creciente del cualquier fluctuación de densidad. Es por ello por lo que estas condiciones no pueden ser naturales y se intentan obtener de forma dinámica, por medio de la hipótesis del periodo inflacionario.
La entropía del universo y la flecha del tiempo
Uno de los problemas más acuciantes con las condiciones iniciales es, según consta en una larga lista de literatura, el problema de la entropía. En concreto, explicar por qué observamos tal grado de orden en el universo. Un simple cálculo vale para mostrar que si toda la materia estuviese concentrada en agujeros negros la entropía sería mucho mayor que la actual, al menos si nuestra noción del concepto de entropía y cómo calcularla es correcta hoy. Dado que la segunda ley de la termodinámica afirma que la entropía en el universo siempre aumenta se nos presenta la pregunta de por qué es la entropía actual tan baja en comparación con la entropía máxima posible que somos capaces de calcular. O, de otra forma, por qué el universo empezó en un estado de entropía muy baja, por qué fueron precisamente esas sus condiciones iniciales.
La cantidad de entropía de un sistema es proporcional al logaritmo de su número de microestados posibles. Si imaginamos una elección de las condiciones iniciales al azar, con una probabilidad uniforme para la elección de los microestados, un sistema con un número finito de grados de libertad normalmente se encuentra en un estado de máxima entropía. La entropía de un sistema en un microestado determinado es nula y si la probabilidad para su elección es uniforme parece más bien improbable encontrar al sistema en un microestado determinado. En este sentido una entropía baja corresponde con algo muy poco natural y sólo a la entropía alta la calificaríamos como una condición inicial natural.
El cerebro de Boltzmann
Hace más de un siglo Ludwig Boltzmann propuso que este estado de baja entropía apareció como una fluctuación dentro de un universo mucho mayor de entropía muy alta. Esto no atenta en contra de la segunda ley de la termodinámica, ya que incluso en un sistema en equilibrio termodinámico pueden existir fluctuaciones aleatorias locales (no en el sistema total) en el nivel de entropía. La mayoría de las fluctuaciones serán pequeñas pero algunas serán mayores. En este contexto aparece la denominada paradoja del cerebro de Boltzmann. El principio antrópico nos exige que al menos exista un observador o una estructura compleja en el seno de esa fluctuación. Por esta razón este principio no es suficiente para explicar la existencia de muchos observadores, ya que la existencia de una fluctuación con uno solo es mucho más probable (al ser una fluctuación menor). Deberán existir muchos universos en lo que sólo deambule una sola mente en ellos.
Este argumento adolece de un problema serio: no considera que la evolución del universo puede llevar de forma natural a la aparición de estructuras complejas una vez acaecidos ciertos hechos. La aparición de millones de observadores o estructuras complejas no tiene en ese sentido que ser más improbable que la aparición de una planta. Los conceptos de probabilidad y evolución temporal empiezan a tomar un caracter sospechoso cuando uno intenta tratar este tema con rigor. El problema de la entropía en el universo es seguramente uno de los más profundos en la física.
En cualquier caso, nos dicen, nos quedamos con el interrogante de explicar el universo como resultado de condiciones iniciales que podamos considerar naturales. Estas condiciones son estados de alta entropía, configuraciones de equilibrio con fluctuaciones ocasionales, las cuales no parecen suficientes para explicar nuestro universo observado. En definitiva, queremos explicar la flecha del tiempo desde un estado de entropía baja a uno de entropía alta.
La diferencia entre descripción macroscópica y microscópica
Sin embargo, no es oro todo lo que reluce. La descripción de un universo en un estado inicial de baja entropía es una descripción macroscópica. Toda descripción macroscópica significa necesariamente un desconocimiento del estado real del sistema. Es decir, no sabemos en qué microestado se encuentra el universo en su estado inicial, desconocemos sus condiciones iniciales. Es por eso por lo que expresamos el macroestado como una serie de microestados posibles, cada uno con una probabilidad asociada a él. Tal probabilidad depende de la información que poseemos sobre el sistema. Una forma de medir este desconocimiento es por medio de la idea de entropía. La entropía es una medida del desorden de un sistema y, en términos de teoría de la información, representa nuestra ignorancia del estado del sistema.
Por otro lado, un sistema microscópico, cuya evolución temporal queda descrita por las leyes de la cuántica, está en un microestado concreto. En un microestado concreto la entropía es nula, ya que el microestado es conocido perféctamente. Con esta reflexión, pienso yo, se empieza a poner un poco el dedo en la llaga de los argumentos anteriores. Si pasamos a un régimen microscópico de descripción, entonces tiene sentido hablar de estados concretos de cada una de las partículas del universo o en concreto de cada uno de sus grados de libertad fundamentales. En tal descripción la entropía es siempre nula. Esto es así porque las leyes fundamentales de la física son reversibles temporalmente, en ellas la entropía se mantiene constante y nula si el microestado es conocido.
En este sentido aparece también una de los frecuentes malentendidos sobre el teorema de recurrencia de Poincaré. Este teorema nos dice que ciertos sistemas acaban por volver a su estado inicial si uno espera tiempo suficiente. Esta afirmación se entiende a veces como una violación de la segunda ley de la termodinámica. Pero está claro que el teorema de recurrencia de Poincaré es un teorema sobre la evolución de un microestado. Es decir, la evolución de un sistema de partículas (por ejemplo) cuyas posiciones y velocidades son exáctamente conocidas en un tiempo dado. El teorema afirma que esta configuración se dará tras cierto tiempo otra vez. La violación de la segunda ley de la termodinámica no es realmente tal: sólo podemos hablar de la segunda ley de la termodinámica cuando hablamos de macroestados. En este caso hablamos de un microestado concreto y la entropía del sistema durante todo el tiempo es nula.
Entropía o no entropía...
En definitiva, ¿existe un problema con la entropía inicial del universo? ¿qué significa la flecha del tiempo? ¿puede ser una ilusión generada por el tipo de descripción? Si es este el caso ¿por qué sufrimos tal ilusión y qué la genera? Ya me gustaría sabelo. Ahí está la gravedad con su naturaleza estadística (el hecho que las ecuaciones de Einstein no sean mas que reflejo estadístico de unos grados de libertad aún desconocidos) que quizás tenga bastante que decir sobre el tema. Esto igual para otra vez. Sirva lo mencionado para reflexionar, porque respuesta no tengo ninguna.
Referencias
La tumba de Ludwig Bolzmann en el Zentralfriedhof de Viena
A moving body whose motion was not retarded by any resisting force would continue to move to all eternity.
Es wird sich alles finden, wenn die Zeit dafür gut ist. S. H.
... I have never believed that reality could turn out to be fixed by an unimaginative initial condition. Bryce deWitt
Ha pasado ya más de medio siglo desde que George Gamow, uno de los pioneros y creadores del modelo del big-bang, planteara junto con Ralph Alpher y Robert Herman la idea de la nucleosíntesis en el marco de este modelo, postulando la formación de elementos ligeros durante una fase muy temprana del universo. Gamow también dió nombre a la substancia inicial de la que debió haber estado compuesto el universo en el instante de la creación. La llamó "ylem", un término procedente del inglés medieval, usado para denominar materia, que llegó al inglés del término griego υλη (hyle, madera). Para celebrar aquel trabajo conjunto, Gamow puso una etiqueta con el nombre de ylem a su botella de licor...
El caso es que el orígen griego del término ylem se remonta a hyle que pasó también a denotar materia, y de tal orígen nos ha llegado el término hilozoísmo. Se trata de una filosofía, de una concepción de la materia y toda la naturaleza que considera que está dotada de vida. El artículo inglés de wikipedia explica el concepto bastante bien: Hylozoism. Al menos en su versión más inmediata esta es una posición difícil de mantener hoy en día, pero no exenta de belleza.
Yo siempre he pensado que la física, y en general la ciencia, debe ser sentida y no sólo pensada para ser entendida. De forma muy ligera es lo que he pretendido algo con las últimas entradas. La reflexión sobre conceptos físicos es también un juego poético, la ciencia es al fin y al cabo una metáfora de la realidad, y estos están ligados a sentimientos y sensaciones. Podría hablar más sobre esto que me ha tenido ocupados mis pensamientos un buen tiempo. Pero lo mejor creo que es incitar a pensar para encontrar el propio camino hacia el cosmos - "a personal voyage" en palabras de Carl Sagan. Y la mejor forma que se me ha ocurrido es con imágenes y citas. Es curioso que una forma de calcular mentalmente es relacionando números con sensaciones e imágenes. Es el método usado por Daniel Tammet (una de las pocas personas con síndrome del sabio - inglés "savant" - capaz de explicar cómo calcula), que mencionaba en una entrevista que el número once es simpático. Creo que es sólo una manifestación de algo mayor, de una conexión espiritual y poética con la realidad.
Pero hilozoísmo es otra cosa, claro. Ya me gustaría a mí saber si el átomo de hidrógeno es simpático o no. Estoy bastante seguro que debe serlo, sencillo y simpático, con capacidad de hacer buenos amigos, algo que nos ha venido muy bien a estructuras tan complejas como nosotros.
For small creatures such as we the vastness is bearable only through love. Carl Sagan
An object is influenced directly only by its immediate surroundings...
Center: (1) A point or place that is equally distant from the sides or outer boundaries of something; the middle (2) A point around which something rotates or revolves (3) A part of an object that is surrounded by the rest; a core (4) A person or thing that is the chief object of attention, interest, activity, or emotion (5) A point of origin, as of influence, ideas, or actions (6)...
But the most impressive fact is that gravity is simple. It is simple to state the principles completely and not have left any vagueness for anybody to change the ideas of the law. It is simple, and therefore it is beautiful. It is simple in its pattern. I do not mean it is simple in its action—the motions of the various planets and the perturbations of one on the other can be quite complicated to work out, and to follow how all those stars in a globular cluster move is quite beyond our ability. It is complicated in its actions, but the basic pattern or the system beneath the whole thing is simple. This is common to all our laws; they all turn out to be simple things, although complex in their actual actions. Richard P. Feynman
When one tugs at a single thing in nature, he finds it attached to the rest of the world. John Muir
La invarianza de Lorentz es un pilar fundamental de la teoría de cuerdas. La acción basada en el área de la hoja de mundo de la cuerda (la acción de Nambu-Goto) es invariante frente a transformaciones de Lorentz, tal y como uno puede leer en los primeros capítulos de cualquier introducción a la teoría. Esta es una simetría fundamental la cual puede ser rota de forma dinámica, espontánea, pero cuya validez como simetría fundamental está en la raíz de la teoría. Pues bien, un único fotón ha venido a revolucionar el mundo de la física teórica estos días en un papel publicado por la colaboración del telecopio Fermi (anteriormente denominado GLAST):
Testing Einstein's special relativity with Fermi's short hard gamma-ray burst GRB090510
Authors: Fermi GBM/LAT Collaborations
Abstract: Gamma-ray bursts (GRBs) are the most powerful explosions in the universe and probe physics under extreme conditions. GRBs divide into two classes, of short and long duration, thought to originate from different types of progenitor systems. The physics of their gamma-ray emission is still poorly known, over 40 years after their discovery, but may be probed by their highest-energy photons. Here we report the first detection of high-energy emission from a short GRB with measured redshift, GRB 090510, using the Fermi Gamma-ray Space Telescope. We detect for the first time a GRB prompt spectrum with a significant deviation from the Band function. This can be interpreted as two distinct spectral components, which challenge the prevailing gamma-ray emission mechanism: synchrotron - synchrotron self-Compton. The detection of a 31 GeV photon during the first second sets the highest lower limit on a GRB outflow Lorentz factor, of >1200, suggesting that the outflows powering short GRBs are at least as highly relativistic as those powering long GRBs. Even more importantly, this photon sets limits on a possible linear energy dependence of the propagation speed of photons (Lorentz-invariance violation) requiring for the first time a quantum-gravity mass scale significantly above the Planck mass.
Esto significa que el fotón en cuestión cumple de forma muy exacta h f / c = p, la relación de dispersión impuesta por la relatividad especial basada en la simetría de Lorentz. Existen teorías con espacio-tiempos discretos que predicen desviaciones de esta relación de dispersión a la escala de Planck. Estas teorías deberían empezar a ponerse en duda frente a este resultado. Lubos Motl defiende vehementemente esta posición en su blog y argumenta sobre la refutación experimental de teorías como la gravedad cuántica de lazos o las triangulaciones dinámicas y a su vez la confirmación de la teoría de cuerdas:
Una característica especial del big-rip es que es producido por un fluído perfecto con parámetro de estado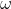 
menor que -1, usualmente denominado energía fantasma, y lleva a una evolución asintótica del factor de escala de forma que este se hace infinito en un tiempo finito.
Es importante notar que esta evolución, al contrario que la evolución provocada por una energía oscura con 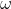mayor o igual que -1 y menor que -1/3, no lleva a una muerte térmica. Intuitivamente podríamos pensar que es así: si la expansión es aún más fuerte que con energía oscura o por ejemplo constante cosmológica, entonces, llevando estas a una muerte térmica, el big-rip llevará con aún más razón a una muerte térmica.
El problema es que este argumento basado en la diluición de la densidad energética, sólo es válido para la energía ordinaria, pero no para la energía fantasma. Todo lo contrario, la densidad energética de la energía fantasma aumenta con el tiempo, llevando a lo que se conoce como singularidad del big-rip (una densidad energética infinita).
Esto es fácil de ver si se considera que de la conservación local de energía 
para un fluído perfecto se obtiene la conocida ecuación
})
Para 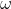menor que -1 está claro que 
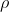va a aumentar a medida que 
aumenta y se hará infinita cuando sea infinito. Más detalles sobre las propiedades de la energía oscura en el famoso papel de Caldwell:
A Phantom Menace? Cosmological consequences of a dark energy component with super-negative equation of state
Cuando uno quiere forzar las ecuaciones de la cinemática relativista para describir una partícula en movimiento con su función de onda, se encuentra con inconsistencias matemáticas. Estas se resuelven en el marco de la teoría cuántica de campos, permitiendo creación y aniquilación de partículas, es decir, pasando a una teoría en la cual la cantidad de partículas no está fijada. La partícula como objeto de estudio queda sustituida por el campo, un objeto complicado, cuyas excitaciones dan lugar a partículas. El hecho de no poder considerar un número fijo de partículas queda claro pensando por ejemplo en el problema de la localización de una única partícula: a medida queremos confinarla más y más y usamos más energía para ello en nuestro experimento de detección, de acuerdo con el principio de incertidumbre el momento de la partícua será cada vez mayor, y, dadas las altas energías involucradas, en la teoría cuántica de campos esto lleva a la aparición de pares de partículas del vacío.
La propagación de excitaciones del campo se denomina propagador. El propagador es una solución a las ecuaciones de movimiento del campo generada por la existencia de una fuente o una perturbación puntual - es lo que se conoce como función de Green de las ecuaciones de movimiento. En la mecánica cuántica no relativista el propagador de la ecuación de Schrödinger nos representa una partícula moviendose de un punto a otro. En la teoría cuántica de campos el propagador no representa una única partícula. De hecho, el propagador es diferente de cero fuera del cono de luz de un evento. Esto significa que la excitación del campo representada por el propagador tiene una probabilidad no nula de existir fuera de su propio cono de luz. Esto no puede representar una partícula ya que de otra forma esta partícula violaría la causalidad. La idea del propagador representando una partícula suele estar algo extendida. Por ejemplo en los diagramas de Feynman vemos líneas internas y pensamos que eso es una única partícula virtual que se intercambian dos líneas externas (partículas reales) para interactuar. Las líneas internas son precisamente propagadores del campo y no representan partículas, sino una suma sobre todos los momentos posibles. En cierta medida una suma sobre una cantidad infinita de estados básicos de partículas.
La causalidad se salva en la teoría cuántica de campos tan pronto uno considera correlaciones entre mediciones. En general cualquier influencia en mediciones está condicionada a quedarse dentro del cono de luz, un resultado famoso (conocido como microcausalidad). Un correlación de mediciones no es un objeto matemático como el propagador, sino algo relacionado con el commutador del campo. Si el commutador del campo en dos puntos diferentes es nulo entonces no existe correlación causal entre esos dos puntos. Y como las partículas son algo medible esto nos asegura que nunca podemos detectar una partícula fuera de su propio cono de luz un instante posterior. Es decir, dada una medición de una partícula en una región del espacio, una medición en otra región causalmente desconectada (fuera del cono de luz de la primera) debe tener probabilidad nula de encontrar la partícula. Este sobrio comportamiento causal en las mediciones se contrapone al comportamiento del propagador y en general de los estados en la teoría. Hay que diferenciar entre estados y mediciones.
Precisamente esta diferencia es esencial en el conocido teorema de Reeh-Schlieder. Este teorema nos dice que si tenemos una región acotada del espacio-tiempo S, la acción de los operadores O(S) (definidos como combinaciones del operador campo sobre funciones suaves en S y nulas fuera de S) sobre el vacío O(S) |0> es densa en el espacio de estados. Esto significa que cualquier medición realizada de forma local en S puede modificar el estado del campo en cualquier lugar del espacio-tiempo; ejecutando experimentos en un laboratorio, podemos crear estados en un lugar arbitrario del espacio-tiempo. Es chocante que este teorema sea consistente con la microcausalidad. Tan chocante que existe una gran cantidad de literatura al respecto. Pero modestamente creo que no lo es. Sólo hay que diferenciar entre estados y mediciones.
En concreto, al hablar de microcausalidad no nos interesan tanto los estados del campo que pueden existir fuera o dentro del cono de luz, sino que nos interesan las mediciones que vamos a realizar con nuestro detector fuera o dentro del cono de luz. Son las mediciones las que vienen fijadas por la condición de microcausalidad y no los estados. El teorema de Reeh-Schlieder nos habla de estados, la microcausalidad de mediciones. La condición de microcausalidad nos indica que dada una excitación del campo medida en x, la medición de otra excitación en en y, con en x, y separados espacialmente (fuera de sus respectivos conos de luz), no puede estar correlacionada con la anterior. Es el propagador del campo el que lo cambia de un estado a otro y con ello parece claro que mientras nos concetremos en los estados las contribuciones fuera del cono de luz van a ser posibles. Al final, sin embargo, estas contribuciones resultan cancelarse cuando uno estudia mediciones.
Este blog está últimamente poco movido pero no puedo pasar sin mencionar el lanzamiento del Planck en día 14 de Mayo, como muy probablemente cualquier lector sabrá de las noticias en los medios de comunicación. El satélite se dirige hacia el punto Lagrange 2 donde empezará a operar. Si nos atenemos a la misión WMAP probablemente los primeros resultados estén disponibles dentro de un año o un año y medio.
No hay decisión definitiva aún para el día del lanzamiento del satélite Planck, el cual será lanzado junto con el telescopio Herschel a bordo del Ariane. La previsión era un lanzamiento a mediados de Abril, en concreto el día 16, pero fue aplazado sin fecha definitiva. La razón parece ser la complejidad del Herschel, según la página de noticias de la ESA:
The Herschel telescope mirror, the largest ever to be launched in space, is a novel and advanced concept using 12 silicon carbide petals brazed together into a single piece; it is one of the major technological highlights of the mission. The complexity of the structure and its uniqueness means great care must be taken to ensure that stresses exerted on it during launch are well understood.
Over the next few days, a panel of independent experts led by the ESA Inspector General and Arianespace will carry out a final cross-check of the documentation to demonstrate that the required safety margins for the telescope are met.
The new launch date will be defined shortly.
Estamos atentos. Información de última hora en: Herschel and Planck launch campaign.
El experimento de Afshar es controvertido ya que su autor afirma refutar con él el principio de complementariedad. Este establece que ambas descripciones, la ondulatoria y la corpuscular, son necesarias para comprender el mundo cuántico, pero lo son de forma complementaria: cuando vale la una la otra no es válida, y al revés. Esta conclusión puede ponerse en duda como veremos a continuación.
Para entender el experimento partamos del experimento usual de la doble ranura.
En este experimento sabemos que si ambas ranuras están abiertas se nos muestra el comportamiento ondulatorio en forma de interferencia en la placa fotográfica a la derecha. Si no obstante somos capaces de determinar en principio y de alguna forma el camino que una partícula ha tomado (ranura S1 o S2), entonces en la placa no aparecerá interferencia y lo que se nos muestra es comportamiento corpuscular.
Imaginemos ahora primero que tras las ranuras ponemos una rejilla. Esta rejilla es tal que sus aberturas corresponden a los picos de interferencia. Esto significa que para el caso de las dos ranuras abiertas la rejilla no atenúa nada la señal final en la placa fotográfica, ya que está dejando pasar los fotones correctos en los picos.
Volvamos al experimento usual de la doble ranuda, sin la rejilla mencionada. Consideremos ahora que detrás de las ranuras ponemos una lente, que actúa de la siguiente forma. Cuando sólo la ranura 1 está abierta, la lente manda los fotones que pasan por ella al detector 1. Cuando sólo la ranura 2 está abierta, la lente manda los fotones que pasan por ella al detector 2.
Ahora imaginemos que juntamos ambas cosas, la rejilla tras las ranuras y la lente tras las ranuras.
Este es el experimento de Afshar. El resultado es que no hay atenuación en la señal de la placa fotográfica. Es decir, que existe interferencia entre las ondas que pasan por cada una de las ranuras.
Asfhar concluye que ocurren estas dos cosas a la vez: existe interferencia debido a la falta de atenuación y existe determinación del camino de cada fotón debido al uso de la lente. Con ello se viola el principio de complementariedad, ya que en un mismo experimento los fotones han mostrado características ondulatorias y corpusculares.
No obstante, esta conclusión no tiene por qué ser correcta. Lo que parece bastante fuera de duda es que existe interferencia. Pero lo que no parece nada claro es que la lente realmente esté determinando el camino en el caso de dos ranuras abiertas. Lo que está probado es que la lente manda los fotones que pasan por la ranura 1 al detector 1 en el caso de estar la ranura 2 cerrada, y al revés. Concluir de esto que existe una determinación del camino para el caso de dos ranuras abiertas es una extrapolación muy probablemente inaceptable.
Para ilustrarlo consideremos un electrón en un estado de superposición de la proyección de su espín sobre el eje z (|up>, |down>), que no obstante, es un estado determinado en el eje x (|s>).
|s> ~ |up> + |down>
Una medición sobre el eje x mostrará que el sistema se encuentra en el estado mencionado |s>. Más tarde, una medición en el eje z hará colapsar el estado en una de las dos proyecciones posibles sobre el eje z, aleatoriamente sobre |up> o sobre |down>. Sin embargo, no nos es permitido preguntar si el sistema estaba realmente en |up> o |down> mientras se propagaba.
En el experimento de Afshar la situación es similar. El sistema, la partícula, se prepara en un estado que es aproximadamente un autoestado de momento. Se propaga en superposición de posiciones, y, si se le deja propagarse así (es decir, si se mantienen ambas ranuras abiertas), la medición de la posición en la placa fotográfica nos muestra que no podemos afirmar nada sobre la posición durante el trayecto. No podemos preguntarnos por qué rendija pasó el electrón, ya que el sistema no está en un autoestado de la base sobre la que proyectamos.
La diferencia en este experimento es que la proyección final del estado de la partícula no es sobre todas las posiciones posibles verticales en una placa fotográfica, sino en lo que Ruth Kastner (en Why the Afshar Experiment Does Not Refute Complementarity) denomina "slit-basis":
En el experimento de la doble ranura el sistema preparado en un estado concreto puede proyectarse sobre todas las posiciones posibles en el eje vertical haciendo uso de una medición de posición con una placa fotográfica. En este caso, haciendo uso de lentes, el sistema puede proyectarse sólo sobre L' y U'. No obstante, estos dos estados básicos no tienen correlación uno a uno con los estados L y U.
Más información en:
http://en.wikipedia.org/wiki/Afshar_experiment
La paradoja de Olbers nos dice que en un universo estático e infinito el cielo nocturno debería ser totalmente brillante sin regiones oscuras o desprovistas de luz. Formular las condiciones de la paradoja con precisión nos ayudará a entenderla mucho mejor.
En concreto, la formulación matemática de la paradoja consiste en calcular el flujo de luz que recibimos estando situados en el orígen de un sistema coordenado esférico. Para empezar establecemos dos hipótesis. La primera hipótesis es que las fuentes de luz se distribuyen de forma homogenea en el espacio. La segunda es que el espacio es estático.
Primero consideramos el flujo de luz que llega a nosotros emitido desde una fuente a una distancia r. En un espacio estático este flujo es proporcional al inverso del cuadrado de la distancia, f ~ 1/r². Luego consideramos la cantidad de fuentes de luz en una corona esférica. Esta cantidad n aumenta con el radio al cuadrado, n ~ r². Por tanto, la suma del flujo de luz de todas las fuentes de luz localizadas en una capa esférica a un radio cualquiera es F ~ f n. Este valor es una constante ya que la dependencia con r se cancela.
¿Cuántas capas esféricas queremos sumar? Empezamos con r = 0 y vamos avanzando a radios cada vez más grandes. Ahora establecemos dos hipótesis más. Primera que el universo es infinito en extensión. Segunda que sus fuentes de luz son eternas. Con ello vemos que la suma de capas esféricas es infinita y que cada capa contribuye con un valor constante (y no infinitésimo) al flujo total de luz. El resultado es por tanto infinito. Esta es la paradoja de Olbers.
Resumiendo, hemos dado con un flujo infinito combinando cuatro hipótesis:
1. Las fuentes de luz se distribuyen de forma homogenea en el espacio
2. El espacio es estático
3. El universo es infinito en extensión
4. Las fuentes de luz son eternas
Vamos a ir desglosando las hipótesis tomadas una a una.
Primera, la homogeneidad de las fuentes de luz. Si la distribución de fuentes no es homogenea la paradoja no tiene por qué darse. Benoit Mandelbrot, el creador de las fractales, propuso una cosmología que solucionaba la paradoja de Olbers precisamente de esa forma. En concreto, en un universo en el cual la distribución de fuentes de luz es de dimensión fractal menor que dos, la paradoja no se da aun en caso de tener infinitas fuentes en un universo infinito cuya existencia es eterna.
La razón es que ya no vale n ~ r² y no va a haber cancelación con f ~ 1/r². Lo que vale en general es que para una dimensión fractal D, n ~ r^{D-1}, haciendo que la paradoja se solucione si D < 2. La justificación de un modelo cosmológico así viene del hecho que a cierta escala las fuentes de luz parecen agruparse en distribuciones fractales en el universo - aunque según me consta a mí los estudios no son concluyentes y no son extrapolables a muy grandes escalas.
Segunda hipótesis, el espacio estático. Si el espacio no es estático ya no se cumple que f ~ 1/r², sino que en general para un universo en expansión el flujo está más diluido. En determinados modelos esto soluciona la paradoja. Esta era la solución del modelo estacionario de cosmología de Hoyle y Burbridge que se basaba en un espacio-tiempo de-Sitter.
Tercera hipótesis, la extensión infinita del espacio. Si el espacio no es infinito y tiene un borde (o digamos que la distribución de fuentes de luz tiene un borde), entonces la suma sobre coronas esféricas se acaba a un radio determinado. Con ello la suma del flujo es finita.
Ahora bien, cuidado, si el espacio es finito pero ilimitado (y el resto de las hipótesis siguien siendo válidas, en concreto la edad infinita de las fuentes de luz), entonces las luz emitida en pasados cada vez más remotos da una o varias veces la vuelta al universo hasta llegarnos. Dado que la edad de las fuentes es infinita la cantidad de coronas a considerar es otra vez infinita y la paradoja no se soluciona.
Cuarta hipótesis, la edad infinita de las fuentes de luz. Esta es evidente: si las fuentes de luz no existen desde un pasado infinito sino desde un tiempo T, entonces, dado que la velocidad de la luz c es finita, la cantidad de coronas a considerar es finita, en concreto hasta un radio R = c T.
Es maravilloso ver como esta paradoja tan simple y cotidiana nos pone frente a un misterio cosmológico sin precedentes y se convierte en una piedra angular de la cosmología, tal y como nos muestra la profundidad de las posibles soluciones a la paradoja. Cualquier modelo sobre el universo debe necesariamente de enfrentarse a ella.
Hace cuarenta años, en 1969, se otorgó el premio Nobel de física a Murray Gell-Mann, por sus descubrimientos sobre partículas elementales. Si hay algo que destaca en la línea de descubrimientos e ideas de Gell-Mann es la belleza y la armonía. El camino óctuple o en inglés eightfold way, es la punta del iceberg del maravilloso mundo de las simetrías en la física de partículas.
Simetrías y cargas conservadas
El universo está lleno de simetrías que son cumplidas por ciertos sistemas. Es decir, existen acciones las cuales, realizadas sobre ciertos sistemas, dejan sus propiedades físicas invariantes. Ejemplo. Imaginemos un condensador con dos placas infinitas conductoras y paralelas la una a la otra, y ambas perpendiculares a un eje z, localizadas en z = - L, z = + L. Entre ellas existe un campo eléctrico paralelo al eje z. Este sistema tiene una clara simetría de traslación en dos direcciones: las dos direcciones x, y paralelas a las placas. La situación es indéntica independientemente de en qué punto x, y nos situemos.
Si uno imagina estas dos placas infinitas, el sistema tiene una simetría de traslación en las dos direcciones perpendiculares al eje z
Uno de los resultados más importantes de la física del siglo pasado es el teorema de Noether. Este nos dice más o menos que para tales simetrías existe siempre una carga conservada. El término carga debemos entenderlo en un contexto general, y no pensar sólo en la carga eléctrica por ejemplo. En el ejemplo anterior, el teorema de Noether nos dice que van a existir dos cargas conservadas, una para cada simetría: una a lo largo del eje x, otra a lo largo del eje y. Estas cantidades conservadas resultan ser las componentes x, y del momento lineal px, py.
Para entenderlo supongamos que entre las placas ponemos un electrón. No existen fuerzas en el plano x, y, y con ello según la segunda ley de Newton el momento lineal px, py del electrón se conserva. La forma de su movimiento es independiente del punto en el plano x, y en el que se encuentra inicialmente. Es diferente al momento lineal en z (pz). Dado que existe un campo eléctrico en z, ocurrirá que pz variará con el tiempo de acuerdo con la segunda ley de Newton. Por contra px, py se mantienen siempre constantes mientras el electrón se mueve entre las placas.
¿Qué valores pueden tomar estas cargas conservadas? Cada una px, py un valor infinito en la recta real. Sea cual sea, este valor se mantiene constante siempre. En definitiva, nada cambia en el electrón y su estado de movimiento por desplazarlo en x, y. Este hecho nos resulta en la conservación de su momentos lineales px, py.
El isospín y la simetría entre neutrón y protón
Una de las brillantes ideas de Werner Heisenberg fue proponer que existe una simetría entre protón y neutrón, tal que nada cambia por intercambiar el uno por el otro. A primera vista esto puede parecer sorprendente, dado que ambos tienen cargas eléctricas y masas diferentes, pero la física trabaja con simplificaciones. La masa entre ambos es muy parecida, por lo que a Heisenberg le pareció razonable pensar en primera instancia que en un universo sin interacción electromagnética el protón y el neutrón serían completamente iguales - incluso la diferencia de masa podría tener su origen en la interacción electromagnética, pensó.
Esta simetría postulada por Heisenberg es realmente expresión de una simetría entre los quarks que componen el protón y el neutrón. Estos son el up y el down (u, d). Su masa es muy parecida, pero se diferencian en la carga eléctrica. ¿Qué tipo de simetría es esta entre u, d? En el ejemplo anterior vimos una simetría de traslación en el espacio, aquí se trata de una simetría de rotación en un espacio interno. En esta aproximación o simplifación debe aparecernos por tanto una carga conservada, a la cual se conoce con el nombre de isospín.
¿Qué valores tomará la carga conservada del isospín? Bien, la respuesta a esta pregunta es uno de los episodios más bellos de la teoría cuántica - y cuya justificación se sale del marco de esta entrada. Las matemáticas nos muestran que al contrario de simetrías de traslación para simetrías de rotación los valores posibles son discretos. Para especificar un estado de isospín hacen falta dos números. La situación es similar al caso del espín. Un electrón por ejemplo tiene espín 1/2 y la proyección de este espín sobre un eje determinado será +1/2 ó -1/2 dependiendo de la orientación del electrón respecto del eje. En el caso del isospín igual y se tiene que tanto u como d tienen isospín 1/2 y la proyección de este son u = +1/2, d = -1/2. Al igual que con la proyección del espín, para la proyección del isospín vale que toma valores -I, -I+1, ... I-1, I, en saltos de 1 desde menos el valor del isospín hasta más el valor del isospín (por ejemplo: -1/2, +1/2 para un isospín de 1/2 y -1, 0, 1 para un isospín de 1).
Proyección del espín para un espín de 1/2, detalles sobre el espín y la teoría de rotaciones por ejemplo en el artículo de wikipedia
A su vez el espín de los quarks es 1/2, tanto del u como del d. A diferencia del isospín el espín no nos permite clasificar en grupos de dos partículas - es decir el u en una de +1/2 y otra de -1/2 dependiendo de la proyección en un eje, ya que esta proyección depende de nuestra elección de los ejes de coordenadas - y la física es independiente de estos. Es decir, la proyección del espín se mezcla en una misma partícula y no está asociada a tipos de partículas. La proyección del isospín, por contra, es en un espacio interno de simetría donde tal libertad no existe en principio.
En definitiva, tenemos dos quarks con dos valores diferentes de la proyección del isospín, y con igual espín. Por contra, tienen diferente carga eléctrica. No obstante, hemos dicho que la interacción electromagnética la vamos a ignorar.
Ahora vamos a construir bariones, que son combinaciones de tres quarks, con igual espín. Que la carga eléctrica sea igual o no en estas combinaciones nos trará sin cuidado. Consideremos primero combinaciones de u, d. ¿Qué combinaciones son posibles? Pues tenemos uuu, ddd, udd, uud. De estas combinaciones, en su estado fundamental las combinaciones uuu, ddd tienen espín 3/2, mientras que las combinaciones udd, uud espín 1/2.
Las combinaciones uud y udd de espín 1/2 corresponden con el protón y el neutrón respectivamente. En estas combinaciones dado que dos quarks son siempre u y d, el valor de la proyección del isospín se hereda del tercer quark. Por tanto tienen isospín 1/2 y la proyección 1/2 y -1/2 respectivamente.
El octeto de bariones
Además de considerar los quarks u, d podemos considerar también el quark s (strange = extraño). Su masa no es tan parecida como las de u, d, pero podemos postular igualmente que en cierta simplificación habría una simetría entre los estados formados por estos tres quarks. Al igual que hemos clasificado los estados de isospín +1/2 y -1/2 obteniendo un grupo de dos partículas con masa muy similar, podemos clasificar los estados de isospín + extrañeza (por convención extrañeza -1 si la combinación tiene un quark extraño, -2 si tiene dos, etc.) y obtener un grupo de partículas con masas similares.
Como hemos mencionado antes, distinguiremos entre aquellas combinaciones de espín 1/2 y aquellas de espín 3/2. Las combinaciones de tres quarks iguales sólo pueden tener espín 3/2. Nos concentraremos en las combinaciones de espín 1/2. Estas son las siguientes.
- Con cero s quarks: uud, udd
- Con un s quark: uus, uds, dds
- Con dos s quarks: uss, dss
¿Qué valores de la proyección del isospín tendrán estas combinaciones? En el fondo está claro. Por ejemplo, uss tendrá uss = +1/2 y dss = -1/2, ambas heredadas del valor de la proyección del isospín de u, d respectivamente. La siguiente tabla nos muestra las combinaciones de espín 1/2 con sus valores de isospín y extrañeza, así como las posibles proyecciones del isospín y los nombres de estos bariones:
Ahora lo que vamos hacer ahora es dibujar estas combinaciones en un plano con eje horizontal con la proyección del isospín I3 y eje vertical la extrañeza S. Obtenemos esto (en esta gráfica están dibujadas además la carga eléctrica Q y la hipercarga Y):
Cualquiera que vea esta clasificación con este diagrama por primera vez no puede mas que sorprenderse de la fascinación de la física de partículas. La belleza de esta clasificación llevó a su inventor, Murray Gell-Mann, a denominarlo eightfold way, camino óctuple, en referencia al noble camino óctuple del budismo. El camino óctuple de Gell-Mann representa el comienzo de la aventura de la física de partículas, una historia de descubrimientos cada cual más bello y profundo.
Otras combinaciones
Clasificaciones similares existen para el caso de bariones con espín 3/2, en cuyo caso se tiene no un octeto sino un grupo de diez elementos, también para mesones (compuestos por un par quark-antiquark).
También se han hecho clasificaciones añadiendo quarks y números cuánticos adicionales. Es decir, además de u, d, s, considerar también los quarks c, b, t. Añadiendo por ejemplo el quark c (charmed, encanto) hay que añadir una dimensión más al diagrama que queda algo así (el subíncie representa la cantidad de quarks c en la combinación) - donde nuestro octeto está en la base:
Las diferencias de masas empiezan a hacer estas simetrías insostenibles y poco útiles, y, además, clasificaciones con más de u, d, s, c, ya no son visualizables.
Uno de los resultados más sencillos y a la vez bellos de la difícil teoría cuántica de campos y la óptica cuántica es que nos muestra que una onda electromagnética clásica, tal y como nos la describe las ecuaciones de Maxwell, debe estar formada por un número indeterminado de fotones.
El campo electromagnético puede expresarse en función de sus modos básicos de excitación con monento determinado, que denominamos fotones. Si el campo está en un estado S en el cual existen exáctamente n fotones, escribimos:
S = |n>
denotando que S es un estado completamente determinado por esos n fotones. Si por contra el campo está en un estado de superposición, podemos escribir:
S = a0 |0> + a1 |1> + ... + an |n>
Esto significa un estado de superposición entre estados de cero hasta n fotones. Es similar a la partícula que puede estar en estado de superposición entre diferentes posiciones posibles en el espacio. Aquí lo mismo, pero en vez de posiciones fotones, como excitaciones básicas del campo electromagnético. Pues bien, el valor esperado - clásico - del campo eléctrico y magnético sólo es diferente de cero si el campo está en un estado de superposición.
Pueden existir conjuntos de fotones sin campo eléctico y magnético, pero para que estos existan y oscilen en una onda, tal y como lo requieren las ecuaciones de Maxwell, y la cual pueda actuar sobre cargas acelerándolas, entonces el número de fotones debe ser indeterminado. Un resultado sencillo - fácil de demostrar haciendo uso de operadores de creación y aniquilación - pero profundo a su vez.
En la mecánica newtoniana el movimiento acelerado de un cuerpo viene definido respecto de una clase o conjunto de sistemas de referencia, concrétamente, todos los sistemas de referencia inerciales. De acuerdo con la relatividad general un sistema así puede ser encontrado de forma local en todo punto del espacio-tiempo. Pero ¿qué determina la existencia de tal conjunto de sistemas?
En la relatividad general ocurre también que lejos de toda masa tales sistemas pueden existir. Esto es debido a que el espacio-tiempo se vuelve plano, el mismo que el de la relatividad especial, donde la clase de sistemas de referencia inerciales representan una clase preferida y en cierta medida absoluta o independiente del resto del universo. De forma equivalente se puede pensar que un cuerpo alejado de toda masa puede adquirir inercia, esa propiedad de todo cuerpo que liga aceleraciones a fuerzas. Esto es debido a que el espacio-tiempo se vuelve plano y la inercia aparece como propiedad absoluta de los cuerpo.
La cuestión es si esto es conceptualmente aceptable. Si postulamos que todas las propiedades del movimiento deben ser expresables en términos observables y de forma dinámica, entonces la posibilidad de una determinación absoluta de los sistemas inerciales va claramente en contra de nuestro postulado. En cierta medida queremos hacer física con el menor bagaje posible en lo referente a artilugio teórico absoluto. La existencia de soluciones sin masas pero con sistemas inerciales en la relatividad general va en contra de esto.
En defintiva, la motivación es lograr que movimientos cinemáticamente equivalentes sean también dinámicamente equivalentes. Esta es una forma de expresar lo que se conoce a veces como principio de Mach. Esto no es así en la mecánica newtoniana. Para ilustrarlo recordemos el ejemplo del cubo de agua que gira. Que el agua suba por la pared del cubo y se hunda en el centro del cubo (concavidad) significa que el cubo gira. En la mecánica newtoniana el cubo gira o es acelerado respecto de la clase de sistemas inerciales. Las fuerzas que actúan sobre el agua aparecen de forma absoluta. De acuerdo con la mecánica newtoniana si todo el universo girase pero el cubo no, entonces sobre el cubo no actuarían fuerzas.
Pero que todo el universo gire y el cubo no es cinemáticamente equivalente a que el cubo gire pero el resto del universo no. De acuerdo con nuestro postulado hay que encontrar por tanto también una mecánica que describa estos dos fenómenos como dinámicamente equivalentes. Es decir, si el universo girase pero el cubo no deberá actuar una fuerza sobre el cubo que será igual que si el cubo gira pero el universo no.
Esta hipótesis proporciona además una nueva perspectiva al problema del péndulo de Foucault. La determinación de la velocidad angular de la tierra que se sigue de este experimento ha de ser equivalente a la determinación de la velocidad angular de la tierra que se puede hacer con experimentos cinemáticos; midiéndo posiciones de estrellas fijas en el infinito. Esto es debido a que movimientos cinemáticamente equivalentes sean también dinámicamente equivalentes.
¿Cómo proceder para encontrar una teoría así? El primer indicio nos lo proporciona el principio de equivalencia. Este nos dice que localmente la fuerza gravitatoria es indistinguible de cualquier otra fuerza inercial. Es decir, localmente un campo gravitatorio es equivalente a una aceleración uniforme. Parece sensato intentar encontrar una teoría en la cual la inercia sea consecuencia de la gravitación. Asumiendo un modelo simplificado en el cual no existen otras fuerzas mas que la gravitación, la condición de que movimientos cinemáticamente equivalentes sean también dinámicamente equivalentes vendrá dada por la condición de que:
En el sistema de referencia comóvil con un cuerpo la fuerza gravitatoria que el resto del universo realiza sobre este cuerpo es nula
La condición parece razonable: si cinemáticamente somos capaces de ponernos en movimiento comóvil con el cuerpo de forma que él está en reposo respecto de nosotros, parece sensato exigir que dinámicamente no actúen fuerzas sobre él. Al fin y al cabo estamos intentando que cinemática y dinámica sean equivalentes. Aunque parezca increible esta es la única condición necesaria para establecer la teoría.
Lo mencionado hasta aquí es la base conceptual del trabajo de Dennis Sciama, físico inglés (1926-1999), sobre este tema. En su artículo:
presenta magistralmente un modelo de teoría así. El artículo es una joya, por lo bien escrito que está, por la forma de proceder, por sus ideas bellas conceptualmente bien fundadas, por sus predicciones y por su sencillez en la presentación.
Para imponer la condición mencionada Sciama considera un universo homogeneo e isótropo cumpliendo la ley de Hubble y en el cuál existe una inhomogeneidad representada por una masa gravitacional M. Este es el "resto del universo" que va a actuara sobre una masa test, en la cual se impone el principio mencionado. El modelo que presenta Sciama es una teoría vectorial de la gravitación. Es conocido que una teoría de la gravitación debe ser tensorial, pero el modelo vectorial sirve para extraer suficientes consecuencias físicas interesantes. Sciama promete el modelo tensorial para un segundo trabajo futuro, pero a mí me es desconocido si ese trabajo realmente existió o no.
Debido a que en el universo existen masas en movimiento respecto de nuestra masa gravitacional test, una teoría vectorial de la gravitación consistirá en un campo gravitoeléctrico E y otro gravitomagnético H sobre la masa test - análogamente a las ecuaciones de Maxwell. El campo total F = E + H será cero en el sistema comóvil de la masa test y esta condición, F = 0, valdrá para derivar la segunda ley de Newton con una expresión no trivial para la masa inercial de nuestra masa (gravitacional) test (véase ecuación (5) en el artículo).
No voy a mostrar aquí los pasos matemáticos, pero son sencillos. Sólo requiren de entender ecuaciones análogas a las de Maxwell. Recomiento encarecidamente leer el artículo al que no lo conozca.
Las consecuencias de la teoría son: (i) la constante gravitacional en un punto del espacio-tiempo depende de la distribución de materia local en tal punto, (ii) la energía total de un cuerpo (gravitacional e inercial) es nula (iii) el principio de equivalencia es una consecuencia de la teoría, (iv) la teoría permite calcular la densidad media del universo, (v) para el universo que observamos la mayor parte de la inercia de los cuerpos viene generada por masas a distancias mayores de 100 Mpc, y otras más mencionadas en el artículo.
Visto esto uno se pregunta si realmente la relatividad general puede ser la teoría clásica correcta de la gravitación. La belleza conceptual del principio de Mach, el cual la relatividad general no implementa consistentemente, es tan grande que parece una pena que el universo no haya hecho uso de él. ¿Qué teorías tensoriales y más realistas hay que incorporen este principio? ¿Cómo difieren de la relatividad general? y ¿están experimentalmente refutadas? Estas preguntas nos ocuparán en una segunda entrada en un futuro próximo.
Dentro del retraso que ha supuesto aplazar el lanzamiento del Planck y el Herschel hasta Abril de este año (previsto estaba inicialmente para el verano del 2008 y luego para Octubre del 2008), parece que las cosas siguen ahora su curso.
La lista de correo de la ESA informa que el Herschel está listo para ser mandado a Kourou en la Guayana Francesa, donde será lanzado. Para el Planck por otro lado se ha acabado una parte del software (proporcionado por el Instituto Max Planck para Astrofísica) para la comparación con mapas previos del fondo de microondas.
Si todo va bien, tendremos lanzamiento el día 16 de Abril.
http://herschel.esac.esa.int/
http://www.rssd.esa.int/index.php?project=planck
[Editado] Desde aquí se podrá seguir en directo en lanzamiento:
http://www.videocorner.tv/
Una pequeña lista de algunos observatorios y lugares de experimentos de física para visitar con google maps:
La descripción que nos da wikipedia sobre el principio holográfico es bastante buena:
El principio holográfico es una conjetura especulativa acerca de las teorías de la gravedad cuántica, que dice que toda la información contenida en el volumen de un espacio puede ser representada por una teoría que yace en la frontera de tal región. En otras palabras, si usted tiene un cuarto, usted puede modelar todos los eventos que ocurren en éste creando una teoría que sólo tome en cuenta lo que pasa en las paredes del cuarto.
En concreto existe una relación entre los grados de libertad del volumen y las areas de Planck en la frontera. La información y los grados de libertad en el interior vienen determinados completamente por la frontera, haciendo del universo algo mucho más simple de lo que en principio podría ser.
Craig J. Hogan, director del Center for Particle Astrophysics en el Fermilab, propone un modelo óptico para estudiar el principio holográfico. Un rayo de luz que es medido en dos puntos, emitido en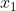 
y recibido en 
, se mueve a lo largo de una geodésica nula. Hogan propone que debido al principio holográfico existe una indeterminación en la posición transversal de la llegada del rayo de luz en :
Cómo llega a esta ecuación es algo que he estado mirando un poco pero no he entendido. La idea parece relacionada con la teoría clásica de difracción (proyectar una rejilla en la frontera en una superficie dentro del volumen). Abajo están las referencias para el que quiera profundizar.
Lo interesante de esta relación es que no está únicamente ligada a la longitud de Planck 
, sino a la distancia entre mediciones, la cual puede tomarse arbitrariamente grande. Con ello, la indeterminación puede crecer dependiendo de esa distancia:
measurement of relative transverse position of two objects separated by macroscopic distance L, at events separated by a null trajectory, yields an indeterminate result. This property implies that measurements of relative transverse positions show a new source of random noise that increases with spatial and temporal separation like 
Hogan afirma que esto debería ser especialmente visible en experimentos de detección de ondas gravitacionales. Precisamente en el GEO600 vienen preguntandose desde hace un tiempo por un extraño ruido cuyo orígen sigue siendo desconocido, y que, según Hogan, corresponde exáctamente con lo predicho por él.
New Scientist tiene esta historia muy bien contada, con comentarios del investigador principal del GEO600: Our world may be a giant hologram.
Lo no entiendo tampoco, y me resulta chocante, es que, siendo que esta indeterminación existe para el desplazamiento transversal de geodésicas nulas, no se haya observado ya en experimentos de óptica. Probablemente hay algo que se me ha escapado, pero tampoco he dedicado demasiado tiempo y esfuerzo a entender los artículos de Hogan. En cualquier caso, de ser esta idea consistente, estamos ante algo realmente intrigante.
