skip to main |
skip to sidebar
En esta entrada vamos a tratar de entender cómo se mueve el sistema solar en nuestra galaxia. Queremos llegar a entenderlo de forma intuitiva y queremos ser capaces de localizar la dirección del movimiento del sistema solar en el cielo nocturno. Para ello tenemos que entender antes algo de teoría.
Primero, hay que mencionar que el sol gira alrededor de el centro galáctico con un período de unos 230 millones de años a una velocidad de unos 220 km/s. Estos números no son conocidos con gran exactitud, pero para hacernos una idea bastarán (ver aquí y aquí para más información). Podemos considerar en primera aproximación, idealizada, que se trata de una órbita circular alrededor del centro de la galaxia.
Pero sabemos por un lado que las órbitas gravitatorias no son circulares en general sino elípticas. Por ejemplo, el movimiento de la tierra alrededor del sol es una órbita elíptica o kepleriana. No obstante, la galaxia no es un cuerpo central esférico sino una distribución de masa con simetría cilíndrica. Esto desvía ligéramente la órbita respecto de una órbita kepleriana. Por otra parte, el sol es gravitacionalmente influido por las estrellas cercanas a él. Todo en uno estas desviaciones del movimiento del sol respecto de la órbita circular ideal son pequeñas y el movimiento puede separarse razonablemente en dos partes (i) un movimiento de traslación circular en torno al centro galáctico y (ii) un movimiento peculiar debido a interacciones gravitacionales que lo desvían del movimiento circular. Definamos con precisión estos dos movimientos.
El Sistema de Reposo Local o Local Standard of Rest (LSR) en inglés es un marco de referencia que se encuentra en una órbita circular alrededor del centro galáctico. El movimiento del Sol con respecto a la dinámica del LSR se denomina movimiento peculiar o movimiento solar básico. Es de unos 16.6 km/s hacia AR = 17:49:58, Dec = 28:07:04. Este valor difiere de una referencia a otra, pero para nuestra precisión un valor de AR = 18:00:00, Dec = 28:00:00 será suficiente. Esta dirección, hacia la que el Sol se mueve con respecto al LSR, se denomina ápex. El ápex a AR = 17:49:58, Dec = 28:07:04 se encuentra en la constelación de Hércules en el cielo nocturno.
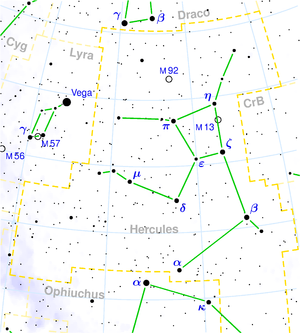
Los valores de AR (Ascensión Recta) y Rec (Declinación) son en coordenadas ecuatoriales, un tipo de coordenadas celestes muy usadas en astronomía que determinan la posición de un objeto en la esfera celeste respecto al ecuador celeste y al equinoccio vernal. Si esto te es desconocido conviene que visites la página de wikipedia sobre las coordenadas ecuatoriales.
El movimiento del sol respecto de las estrellas cercanas, dentro del LSR, se establece midiendo la velocidad radial de las estrellas en la vecindad solar. El resultado, por ejemplo, el valor dado anteriormente, depende de la profundidad de la muestra (el número de estrellas usado para la media), y las clases espectrales de las estrellas seleccionadas (que da lugar a mayor o menor dispersión de la muestra). Para evitar esta incertidumbre en esta definición tan importante, los astrónomos han definido un marco respecto del cual el movimiento solar es de 20 km/s hacia AR = 18:00:00.0, Dec = 30:00:00. Este marco se denomina LSR cinemático (kinematical LSR) y el movimiento del sol dentro del LSR cinemático se denomina movimiento solar estándar. Estríctamente el LSR mencionado anteriormente, respecto del cual el sol se mueve con unos 16,6 km/s hacia AR = 17:49:58, Dec = 28:07:04 se denomina LSR dinámico (dynamical LSR). A pesar de que el LSR cinemático es el más utilizado, vamos a olvidarnos de él y centrarnos en el LSR dinámico que es más intuitivo de entender.
Observemos la siguiente imagen:
Esto se supone que representa la mitad de la galaxia, con el núcleo galáctico y centro a la derecha. El LSR se mueve en una órbita circular alrededor del centro galáctico. Por otra parte, dentro de o respecto del LSR, en el recuadro pequeño, el sol tiene su propio movimiento peculiar con su velocidad peculiar. Para entender mejor el movimiento del LSR debemos echar un vistazo a las coordenadas galácticas. El siguiente dibujo da una idea de este sistema coordenado:
Estas coordenadas se definen de tal modo que la longitud LII = 90 apunta en la dirección de la rotación de la galaxia. La latitud BII = 0 corresponde con el plano galáctico. De este modo, el LSR se mueve hacia LII = 90, BII = 0. ¿Dónde está esa dirección ubicada en el cielo nocturno? Esta dirección corresponde en el cielo con la constelación del Cisne. Para comprobarlo podemos ir a esta página donde podemos convertir las coordenadas ecuatoriales de la constenación del Cisne (aprox AR = 20:62h, Dec =+42:00) a galácticas. Por medio de esta página podemos comprobar también la orientación de la eclíptica (el plano del movimiento de la tierra alrededor del sol) respecto del plano galáctico. Del dibujo de las coordenadas ecuatoriales en el enlace mencionado de wikipedia, vemos que la normal a la eclíptica se encuentra a AR: 16.00.00 y Dec: 66.5h. Insertando en la calculadora se tiene LII= 99.8 BII= 41.3, es decir, la normal apunta casi en la dirección del movimiento del sol.
Así llegamos a nuestro primer resultado: el sistema solar se mueve en órbita circular con el LSR hacia la constelación del Cisne, a una velocidad de unos 220 km/s y con la eclíptica orientada de forma casi perpendicular a su movimiento de traslación.
Además, hemos visto que el sistema solar se mueve dentro de o respecto del LSR hacia la constelación de Hércules con una velocidad de unos 20 km/s. Ahora queremos comparar las dos velocidades.
En primer lugar, es evidente que la peculiar velocidad del sol es pequeña si se compara con la velocidad circular (menos del 10%). En segundo lugar, nos gustaría saber la dirección del peculiar movimiento en coordenadas galácticas. Para ello tenemos que convertir las coordenadas ecuatoriales del ápex en coordenadas galácticas. Para ello volvemos a la página mencionada e insertamos AR = 18:00:00, Dec = 28:00:00, para obtener más o menos LII = 54.00 y BII = 23.00. Si observamos la figura anterior, teniendo en cuenta que LII = 90, BII = 0 es la dirección de movimiento del LSR, se puede ver que el movimiento peculiar del sol, LII = 54.00, BII = 23.00, tiene un componente en la misma dirección que el movimiento del LSR, otro componente hacia el centro galáctico y otro componente hacia el polo norte galáctico:
El movimiento vertical respecto del plano galáctico es interesante ya que el sol resulta tener un periodo de oscilación de varios millones de años respecto del plano galáctico. Este movimiento se ha especulado como causa de extinciones masivas, postulándose el paso por el plano galáctico como causa de perturbaciones de la nube de Oort y el consiguiente bombardeo del interior del sistema solar con cometas. El movimiento horizontal respecto del plano galáctico es consecuencia de la simetría cilíndrica de la galaxia, que hace que las órbitas deban ser modeladas por medio de epiciclos en general (más información por ejemplo en An Introduction to Modern Astrophysics, Carroll & Ostile).
Hemos situado las direcciones del movimiento del LSR y peculiar en el cielo y las hemos comparado, tanto en coordenadas ecuatoriales como galácticas. Ahora queremos saber cómo se mueve el sistema solar hacia el ápex ¿se mueven hacia arriba, hacia abajo, hacia la izquierda, hacia la derecha, etc? Evidentemente estos términos no tienen ningún significado en el espacio exterior, pero podemos preguntarnos con sentido sobre el movimiento del sistema solar respecto del plano de la eclíptica (el plano de la órbita terrestre alrededor del Sol).
Lo que queremos saber es el ángulo entre la dirección normal al plano de la eclíptica y la dirección el ápex. Sea R1 la dirección celeste del polo norte (Dec = 90:00:00). Sea R2 la dirección celeste hacia el ápex (AR = 18:00:00, Dec = 28:00:00). Sea R3 la dirección celeste de la normal a la eclíptica. Estos tres vectores cortan la esfera celeste en tres puntos que forman un triángulo esférico. Sabemos que el ángulo entre R1 y R2 es 90-28 = 62 grados. Sabemos que el ángulo entre R1 y R3 es igual a la inclinación de la eclíptica que son 23.5 grados.
Aplicando trigonometría esférica:
cos(R2 - R3) = cos(R1 - R3) cos(R1 - R2) + sin(R1 - R3) sin(R1 -R2)
(R2 - R3) = arccos [cos(23.5) cos(62) + sin(23.5) sin(62)] (R2 - R3) = 40
En definitiva, nuestro sistema solar se mueve hacia la constelación de Hércules con un ángulo de 40 grados respecto de la normal a la eclíptica:
Cotidianamente el término "vacío" se usa para denotar algo sin un contenido determinado. Los anglosajones usan aquí la palabra "empty". Por otro lado, en la física teórica el término "vacío" tiene un significado muy preciso dependiendo del contexto. Los anglosajones usan aquí la palabra "vacuum". En castellano no usamos habitualmente dos palabras para diferenciar entre estos dos conceptos y caemos a veces en la confusión de mezclarlos. Veamos qué diferentes significados que se le da a este término y qué contexto aparecen.
El vacío en la teoría cuántica de campos
En la teoría cuántica de campos el término "vacío" se usa para denotar el estado sin partículas de un campo cuántico. En general, en la teoría cuántica de campos los campos quedan descritos por una colección o serie de osciladores armónicos cuyos modos de oscilación posibles corresponden en principio con todas las longitudes de onda posibles. Esto se sigue del mero hecho de modelar el comportamiento del campo como una superposición de ondas a distintas frencuencias, y asumir unas ecuaciones de movimiento a nivel clásico. Para más información véase El efecto Casimir y la energía negativa. En un estado así el campo existe y tiene propiedades muy concretas, pero lo que no hay son excitaciones de él que den lugar a partículas propagándose.
Este vacío no puede estar sin contenido alguno. Esto es así porque todo campo fluctua y es una superposición de modos de oscilación fundamentales. Estos modos de oscilación sin embargo no son partículas como las que podemos medir en el laboratorio, pero contribuyen a la energía del vacío y son con ello físicos (más detalles sobre esto en la entrada mencionada anteriormente). Esto hace que el vacío mismo tenga una energía y, con ello, en cierta medida no esté libre de contenido. En defintiva, el "vacío no está vacío" o en inglés, "vacuum is not empty".
En realidad el vacío es un concepto muy sutil y curiosamente dependiente de la aceleración del observador. Lo que para un observador es vacío no tiene por qué serlo para otro en espacio-tiempos curvos o sistemas acelerados. Este es el orígen del efecto Hawking.
El vacío en la relatividad general
En la relatividad general el término "vacío" se usa para denotar soluciones sin materia o sin campo alguno a las ecuaciones e la relatividad general. Aquí se trata de una situación en la que sólo hay un espacio-tiempo. Es importante notar que este espacio-tiempo puede ser plano, sin gravitación alguna, pero también puede tener singularidades u ondas gravitacionales, etc., en definitiva, cualquier propiedad geométrica siempre y cuando no tenga materia. En este sentido esta definición se ajusta mejor a la cotidiana, ya que el espacio-tiempo se puede considerar o imaginar aquí como el recipiente y la materia como su contenido.
En general tanto los campos cuánticos como el espacio-tiempo son algo que existe en todo lugar. Existen ambos no sólo ahí donde no hay partículas, sino también donde las hay. Es decir, el espacio-tiempo es un contínuo sobre el cual o en el cual se encuentra la materia. La materia a su vez queda descrita como un continuo que puede ser excitado para dar lugar a partículas.
Por último mencionar que una descripción rigurosa del estado vacío del campo gravitatorio, como su estado de mínima energía con cierto contenido energético, es algo desconocido. Esto es porque no tenemos aún una teoría cuántica de la gravitación que esté bien fundada y probada. Si queremos aplicar este concepto a la gravitación debemos alejarnos del uso del término "vacío" que se hace en la relatividad general, ya que sólo será vacío aquel estado de mínima energía del campo y no cualquier estado falto de materia. La situación es análoga a por ejemplo la electrodinámica: el vacío en ella es un estado sin campos creados por cargas, pero también un estado sin ondas propagándose. Es luego en la cuántica en la que este estado se nos muestra como algo que fluctua y puede tener un contenido energético.
Cotidianamente diremos que esta copa está vacía. No tiene sin embargo vacío en su interior. En la física cuántica diremos que la copa, incluso si tuviese vacío en su interior, nunca podrá estar vacía
(Editada el 5 de septiembre de 2008: addendum al final)
¿Por qué observamos el espacio con extensión pero el tiempo no? En esta entrada vamos a intentar una respuesta a tal pregunta aparentemente tan sencilla, cosa que además nos servirá de pretexto para tocar de refilón el tema de la causalidad en la relatividad.
Esta entrada es el resultado de una discusión en los foros de la web de física que tenía como intención una definición rigurosa de observar con extensión además de la diferenciación en este aspecto entre espacio y tiempo. No considero que la dada sea una explicación acabada del todo, y creo que aún se le podría sacar algo de partido a este tema o a esta pregunta aparentemente tan sencilla.
Empecemos con la causalidad en la relatividad. En la relatividad especial un evento sólo puede ser influido por eventos que se encuentran dentro de su cono de luz. Esto es una consecuencia de la velocidad finita de la luz, como velocidad máxima de propagación de efectos a partir de sus causas. Como su nombre indica el cono de luz tiene forma de cono con vértice en un evento determinado P (OBSERVER en el dibujo de abajo) como muestra el diagrama de abajo para el caso de dos dimensiones espaciales.
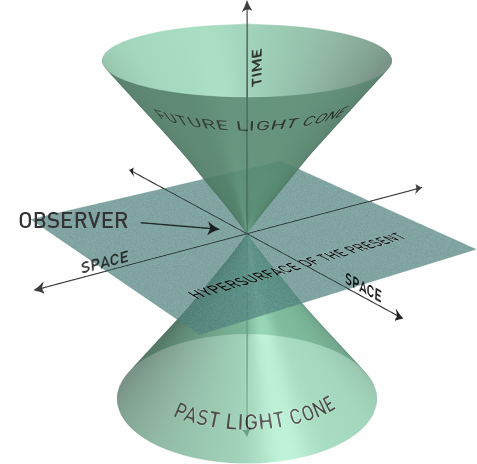
Un evento cualquiera es un punto en el espacio-tiempo que puede o no puede afectar a P. Si le afecta, es porque está dentro de su cono de luz. Le afectará en un instante determinado, pero no le afectará antes o más tarde, al tener el cono de luz forma de cono. La existencia de conos de luz da lugar a la posibilidad de ecuaciones diferenciales hiperbólicas que permiten formular problemas de valores iniciales bien definidos. Por ejemplo, la ecuación de onda. La solución en un punto determinado P a la ecuación de onda depende de los puntos dentro del cono de luz de P. Los puntos exteriores al cono de luz de P no afectan la forma de la solución de la función de onda en P.
Esta observación quizás trivial viene mejor ilustrada considerando en analogía un espacio en el cual los conos de luz no existen. Por ejemplo, el espacio euclídeo sin tiempo. En él las ecuaciones diferenciales son elípticas, como por ejemplo la ecuación de Laplace. En la ecuación de Laplace una solución en un punto determinado viene determinada por los valores de la solución en cualquier esfera con centro en ese punto. Esto es una consecuencia del conocido teorema de Gauss. Si definiesemos un punto en ese espacio como evento, todos los eventos de ese espacio afectarían a todos los eventos, constantemente y siempre.
Por otro lado, conviene notar cómo se comportan los conos de luz en un supuesto espacio en el cual la velocidad de la luz es infinita. En tal caso la generatiz del cono está inclinada noventa grados respecto del eje temporal y es paralela a los ejes espaciales. Esto significa que un evento P es afectado simultaneamente por todos los eventos localizados a un tiempo constante, o, equivalentemente, en la misma sección espacial del espacio-tiempo. Esta es la aproximación newtoniana que se aplica en nuestra vida cotidiana.
La relación de la noción de cono de luz con la de predictabilidad es digna de mención. En general, una definición de simultaneidad distante debe especificar los puntos del espacio-tiempo que se encuentran en una misma sección espacial (véase esto y esto). Los espacio-tiempos causalmente bien definidos son tales que contiene una sección espacial en la que se pueden definir las condiciones iniciales de todo problema de valor inicial que cubra todo el espacio-tiempo. Esto es la definición de superficie de Cauchy. Equivalentemente una superficie de Cauchy es una sección del espacio-tiempo por la cual pasa de un lado a otro de la superficie toda curva temporal una y sólo una vez. La figura siguiente muestra una superficie de Cauchy, que es, por ejemplo, el plano paralelo a xy, donde se encuentra el punto P. Si no hay curvas temporales cerradas todas las curvas temporales de los puntos en el espacio-tiempo (aquí: espacio de dos dimensiones y espacio-tiempo de tres) pasan una y sólo una vez por la superficie de Cauchy (el plano de dos dimensiones paralelo a xy). Existen otras superficies de Cauchy, de hecho existen infinitas, por ejemplo el mismo plano xy.
Vemos en la figura de arriba que para curvas temporales normalitas podemos definir superficies de x constante o y constante que sean cortadas dos veces por las curvas, sin que con ello peligre la causalidad. Pero las superficies de tiempo constante no pueden ser cortadas dos veces por la misma curva temporal. La definición de un problema de valores iniciales bien definido necesita por tanto de una clara diferenciación o asimetría entre espacio y tiempo. Los espacios con conos de luz como el de la relatividad especial tienen esta característica (relacionada por otro lado claramente con la signatura de la métrica). La especificación de los valores iniciales para cualquier evolución temporal bien definida debe ser realizada en una sección espacial del espacio-tiempo.
Lo que queremos explicar no obstante es una característica que es más bien observacional: el espacio lo consideramos o vemos como extenso, pero el tiempo usualmente no. En mi opinión la observación en extenso de algo es una consecuencia de la velocidad tan grande de la luz a efectos cotidianos. Es decir, observar algo con extensión sería sólo una apariencia, resultado de que nos veamos cotidianamente inmersos en un mundo gobernado por la mecánica newtoniana. Para poder precisar esto necesitamos una definición de lo que entendemos por considerar o observar algo extenso.
Consideremos la siguiente definición de observar algo en extenso:
Observo algo con extensión si observo simultaneamente sus extremos.
Esto es posible para un segmento espacial, ya que la luz se mueve en la horizontal en la aproximación newtoniana. Sin embargo, es imposible para un intervalo temporal, precisamente porque la luz se mueve en la horizontal. Esta definición refleja el hecho que podamos observar lo espacial como extenso y que lo temporal nos parezca inextenso.
La explicación también parece ser consistente con la interpretación usual que sólo existe el presente y el pasado y futuro no existen. Esta interpretación o ontología de la teoría es sin duda aplicable en la mecánica newtoniana, pero puede ponerse en duda en un marco de la relatividad especial, en la cual el pasado de alguien puede ser presente de otro debido a la relatividad de la simultaneidad.
En un marco relativista la situación es diferente. Un observador para el cual la luz se moviese muy despacio ¿observaría también el espacio con extensión y el tiempo sin extensión? Imaginemos las dos siguientes situaciones. Ambas por un lado en un marco de la relatividad especial con una velocidad finita de la luz, y, por otro en un marco de la mecánica newtoniana con una velocidad infinita de la luz. Las situaciones pretenden describir una situación análoga para el eje temporal y para el eje espacial en un espacio-tiempo de dos dimensiones. En todas las situaciones nosotros estamos localizados en x = 0.
Primero, dos extremos espaciales de algo A y B.
Para el caso newtoniano recibimos luz de sus extremos simultaneamente:
Diferentes extremos espaciales en la apoximación newtoniana
Para el caso con velocidad finita de la luz recibimos luz de sus extremos en dos instantes diferentes de tiempo:
Diferentes extremos espaciales en la relatividad especial
Segundo, una duración temporal de algo con extremos temporales 1 y 2.
Para el caso newtoniano recibimos luz de sus extremos instantaneamente para el instante 1 y luego para el 2:
Diferentes extremos temporales en la apoximación newtoniana
Para el caso con velocidad finita de la luz recibimos luz de sus extremos en dos instantes diferentes de tiempo:
Diferentes extremos temporales en la relatividad especial
Desde el punto de vista relativista la situación es algo sorprendente, porque la situación es simétrica desde el punto de vista observacional para el eje temporal y para el espacial. No obstante, algo hay que nos permite identificar A y B con los extremos de, por ejemplo, una barra, o en definitiva un objeto que existe a lo largo del tiempo, pero, sin embargo, nada nos permite identificar 1 y 2 como los extremos temporales de algo que existe a lo largo del espacio. Por ejemplo en x = 0 podemos decir que estamos escuchando los diez segundos que dura el sonido de nuestro reloj para despertarnos, pero el mismo sonido a cierta distancia de nosotros no es "el mismo", sino otro al provenir de otro reloj diferente que está alejado.
En el caso newtoniano parece más claro que podamos identificar A y B con los extremos de una barra y no podamos identificar 1 y 2 como los extremos temporales de algo que existe a lo largo del espacio. La observación de los extremos A y B es simultanea para nosotros, cosa que nunca puede ocurrir con 1 y 2. Esto se ajusta bien a la definición de observar con extensión dada. Adicionalmente, el hecho que todo fluya en el tiempo irremediablemente en una dirección da lugar a la situación que tras observar 2 nunca podamos volver a observar 1 otra vez. En el caso relativista este hecho no cambia prácticamente las cosas, ya que al igual que podemos recibir luz desde diferentes valores de t proveniente de A y B, podemos recibir luz desde diferentes valores de x proveniente de 1 y 2.
Para finalizar mencionar que esto, especialmente la definición dada, es una interpretación mía y con mucho gusto la discutiré con quien quiera ponerla en duda.
Addendum 5 de septiembre de 2008:
A veces las cosas son más sencillas de lo que parecen. Creo que el rollo anterior no viene al caso y es completamente prescindible. La razón de que observamos al tiempo inextenso y al espacio extenso está realmente en que todo fluye en el tiempo en una misma dirección.
Las reflexiones que hice antes en este tema son relacionadas de alguna forma con la noción de extensión espacial, pero creo que fallé en identificar ese punto como el esencial. Creo que hay una forma muy sencilla de entender la relación del paso del tiempo con su inextensión.
Como definición de observar algo con extensión tomaré la misma que tomé antes: observo algo con extensión si observo simultaneamente sus extremos. En un diagrama de espacio-tiempo para una dimensión espacial tal cosa puede representarse así:
Las líneas a trazos son rayos de luz que provienen de los extremos de algo que se encuentra en t = 0 y que observamos simultaneamente más tarde. Ahora bien - y esto creo que es una observación lamentablemente sencilla que no veo cómo no se me ocurrió antes - para que la misma cosa sea posible con el tiempo, debería ocurrir que:
Es decir, la luz (el rayo de arriba) debería viajar hacia atrás en el tiempo o fluir en contra de los demás objetos que van siempre hacia valores de t mayores.
El día 12 de junio hizo noventa años del nacimiento de Christie Jeyaratnam Eliezer, un físico matemático prácticamente desconocido pero de interesante biografía. Eliezer murió en marzo del 2001 y dejó tras de si una larga trayectoria científica en Inglaterra, Sri Lanka y Australia. La entrada de wikipedia sobre Eliezer nos da una breve esbozo de su vida.
Su identidad tamil determió gran parte de su actividad, apoyando el movimiento pacífico para la independencia tamil en Sri Lanka. Eliezer estudió en Cambrige, donde su tesis doctoral fue dirigida por Dirac. Más tarde regresó a Sri Lanka donde ocupó la cátedra de matemáticas de la Universidad de Ceylon de entonces separada en varias universidades en 1978. Desde finales de los cincuenta hasta finales de los sesenta estuvo al frente de la facultad de ciencias de la universidad de Malasia en Kuala Lumpur. Por último, fue profesor de matemáticas en La Trobe University de Victoria en Austrialia.
El aspecto de su trayectoria que más nos interesa en esta entrada de mi blog es su trabajo sobre la estabilidad del átomo de hidrógeno con Dirac. El mismo Eliezer lo describía así (de aquí):
After months of my preliminary reading, Dirac suggested that I look into the hydrogen atom problem, with radiation taken into account. From the family of mathematical solutions, one had to select a physically acceptable solution.
I first tried the three-dimensional case, then the two-dimensional and finally the straight line case where an electron is projected towards a stationary proton. I had expected (and so had Dirac) that one would get different solutions with the electron hitting the proton in different ways...
Methods of solving non-linear differential equations were not well known in those days. I was foolish enough to think that an exact solution could exist, but I could not find one. I wrote off to Miss.M.L.Cartwright and Professor J.E.Littlewood for advice. Both of them very kindly helped. It turned out that the electron got stopped before it could reach the proton.
I told this to Dirac, and he seemed surprised. Then he asked the obvious question which foolishly I had not asked myself. What does the electron do after it gets stopped? At the spur of the moment, I said: 'The electron would start moving outwards, then come to a halt, and move back towards the proton and get stopped, probably closer to the proton, and continue this oscillating motion till it falls into the proton'. Dirac's face lit up with pleasure. That is a very beautiful solution, he said.
I left the room in high spirits. But my elation was short lived. When I worked out the equation, I found that the electron, after its first stop, would move away from the proton in a run-away type solution. At the earliest opportunity, I met Dirac again and told him. He said he too had worked it out and come to the same conclusion. Write up what you have in a paper, he said. That paper was published in the Proceedings of the Cambridge Philosophical Society (1943)
Lo que Eliezer fue capaz de probar es ni más ni menos que la estabilidad clásica del átomo de hidrógeno. Todos sabemos de los libros de texto que la física clásica no podría explicar la estabilidad del átomo de hidrógeno, ya que el electrón acelerado emite radiación, y la consiguiente pérdida de energía lo debería hacer colisionar contra el protón alrededor del cual orbita. Los libros de texto nos explican que la mecánica cuántica fue capaz de solucionar este problema al ser la función de onda del electrón en el átomo estacionaria y el valor de expectación de la velocidad del electrón nulo.
Pero independiéntemente de si la conclusión sobre el colapso clásico del electrón es correcta o no, el argumento para llegar a ella que nos muestran ingénuamente los libros de texto no es correcto porque ignora la reacción de la carga (el electrón) a su propia radiación. Lo que Eliezer mostró en los años cuarenta es que asumiendo que la reacción a la radiación viene dada por la fórmula de Dirac-Lorentz (o Abraham-Lorentz), el electrón no colisionará nunca con el protón, y el átomo será estable sin necesidad de introducir la cuántica. Se sabe no obstante que la fórmula de Dirac-Lorentz predice situaciones clásicas inaceptables, por lo que se puede poner en duda las conclusiones de Eliezer.
En cualquier caso, mi impresión (personal) es que el problema de la estabilidad del átomo de hidrógeno sirvió como uno de los muchos pretextos para introducir la cuántica a principios de siglo, pero creo que todavía hoy no está claro si puede existir una solución clásica al problema debido precisamente al problema de analizar clásicamente la reacción a la radiación. Un problema extremadamente complejo.
Hace unos meses, que será ya casi más de un año, tuvimos un debate interesante en los foros de la asociacionhubble.org sobre la función de onda del fotón. La discusión rondaba en torno al famoso libro sobre mecánica cuántica de Francisco José Ynduráin. Queríamos saber si la afirmación del libro sobre la existencia de una función de onda para el fotón era una afirmación soportada por algún argumento riguroso, o si se trataba sólo de un recurso didáctico. Dejando de lado detalles técnicos de esta discusión, el caso es que para aclarar la situación mandé un email a Ynduráin, el cual me contestó muy amablemente.
Después de un corto pero interesantísimo intercambio de emails tras su primera respuesta, Yunduráin se ofreció a mandarme por correo postal su libro mecánica cuántica relativista, editado, pero aparentemente nunca puesto a la venta, y, del cual, según me dijo, tenía varias montañas de ellos en su despacho. Me sorprendió muy agradablemente la sincera intención de ayudar de forma desinteresada. El libro lo recibí en un par de días en casa, muy contento de haber contactado con alguien tan dispuesto a ayudar pese a mi nula relación con el mundo académico de la física teórica.
Cómo son las cosas, que tras un intercambio de emails que vino después, resultó inesperadamente que el pasado zaragozano de Francisco José Ynduráin, el cual vivió hasta los 26 años en la cuidad de Palafox, se había cruzado con el pasado familiar mío. Una sorpresa inesperada en un mundo que es como un pañuelo. "Die Ewigkeit sitzt am Ufer des Augenblicks die Zeit schlägt Brücken", la eternidad se encuentra en la orilla del instante, el tiempo crea puentes, son sugerentes palabras del escritor austriaco Ernst Ferstl para recordarnos que el tiempo trae, pero también se lleva.
Francisco José Ynduráin ha fallecido hace una semana (el viernes 6 de junio) a los 67 años. Yndurán fue una de las figuras más relevantes de la investigación y docencia de la física teórica en España. Su entrada de wikipedia:
¿Qué es lo que encontramos en el universo en el espacio entre planetas, estrellas y galaxias? Esta es una pregunta cuya respuesta depende de la escala que se considera. Vayamos por tanto desde lo más pequeño hasta lo más grande.
Entre planetas: el medio interplanetario
En el sistema solar, entre sus planetas, asteroides, etc., encontramos lo que se conoce como medio interplanetario, de una densidad de una docena de partículas de polvo por centímetro cúbico. Está formado básicamente por polvo que da lugar al fenómeno de la luz zodiacal, y también por un plasma caliente del viento solar.
El campo magnético de la tierra nos apantalla frente al viento solar y la atmósfera de la tierra frente al polvo interplanetario. Este medio por tanto no se encuentra a escalas menores en nuestro planeta.
La luz zodiacal a lo largo de la eclíptica creada por la luz solar reflejada en las partículas de polvo del medio interplanetario
Entre estrellas: el medio interestelar
Ahí lo que hay es el medio interestelar, con varias fases de densidad y composición. Hay regiones frías de polvo con unas mil partículas por centímetro cúbico. Hay también fases muy calientes en los interiores de las burbujas generadas por supernovas a temperaturas de un millón de grados y con unos 0.001 partículas (protones, electrones, etc.) por centímetro cúbico. Y hay también fases intermedias que suelen ser las regiones de HI o las de HII cerca de las estrellas, con densidades desde una a cien partículas por centímetro cúbico.
Una región HII del medio interestelar
El viento solar genera una presión que expulsa el medio interestelar de la región interplanetaria. Con ello este medio no se puede encontrar entre planetas sino únicamente a escalas mayores que planetas.
El viento solar crea la helioesfera e impide que el medio interestelar penetre en el sistema solar
Una interesante entrada en este blog sobre el medio interestelar:
Entre galaxias: el medio intergaláctico y el medio intracumular
Aquí hay algo conocido como medio intergaláctico y también algo usualmente conocido como medio medio intracumular.
El término medio intracumular refiere a un gas caliente a 10^7 K, con unas 0.001 partículas por centímetro cúbico emitiendo rayos-X, y que se encuentra envolviendo los cúmulos galácticos en un equilibrio hidroestático en ellos.
El medio intracumular en el cúmulo Abel 2199
El término medio intergaláctico refiere a lo que se encuentra entre las galaxias y no es medio intracumular. Su composición depende del desplazamiento al rojo. En el universo actual existen filamentos y paredes (en los que se encuentran también los cúmulos galácticos) con un medio intergaláctico de una temperatura algo menor que el medio intracumular y densidad algo mayor. Por otro lado, fuera de los filamentos, existen grandes vacíos de densidad muy baja aunque no vacíos del todo.
Simulación del medio intergaláctico en filamentos a desplazamientos al rojo bajos
A desplazamientos al rojo algo más altos la cantidad de cúmulos galácticos disminuye, ya que el colapso gravitatorio de muy grandes estructuras no ha empezado. El medio intergaláctico ahí está formado básicamente por las denominadas nubes de Lyman-alfa con HI.
Similar al caso anterior, el medio interestelar dentro de las galaxias básicamente impide que el medio intracumular entre en ellas. El medio intracumular y el intergaláctico se encuentran por tanto únicamente a escalas mayores que las galaxias.
Una interesante entrada en este blog sobre el medio intergaláctico a desplazamientos al rojo bajos:
Hasta aquí la materia bariónica.
Entre galaxias y en la galaxia: la materia oscura
A escala galáctica e intergaláctica existe también una gran cantidad de materia no-bariónica (materia oscura). Esta envuelve toda la galaxia en un halo. La composición de esta materia es desconocida y sólo es postulada debido a observaciones indirectas. Promediando a grandes escalas la densidad media de la materia oscura es diez veces mayor que la de toda la materia bariónica.
La materia oscura penetra en la galaxia y debería envolvernos también a nosotros en el sistema solar. Esto es así porque los medios anteriores no interactúan con ella y la presión que ejercen no le afecta. La materia oscura es no-bariónica y no responde a la interacción electromagnética. Su distribución a gran escala es similar a la de la materia bariónica, ya que esta última sufrió colapso gravitatorio precisamente en las regiones en las que preexistía materia oscura.
La distribución de materia oscura a gran escala
En todo el universo: la energía oscura
También se cree que existe energía oscura. Esto es algún tipo de energía o campo que permea el espacio a todas las escalas de forma homgenea e isótropa. Igualmente la composición de esta energía es desconocida y sólo es postulada debido a observaciones indirectas. Promediando a grandes escalas la densidad media de la energía oscura es dos o tres veces mayor que la de toda la materia (bariónica y oscura).
Se cree que la energía oscura se encuentra en todas las escalas y todos los lugares del universo, distribuida de forma homogenea e isótropa. Con ello, llegamos por último a los fondos de partículas.
El orígen de la energía oscura y la constante cosmológica, un misterio para la física desde hace casi un siglo
En todo el universo: los fondos de partículas
Por último todo el universo está lleno de varios fondos de partículas cuya densidad energética media es muy baja. Uno de ellos es un fondo homgeneo e isótropo de fotones, conocido como fondo cósmico de microondas, con unos 400 fotones por centímetro cúbico. Otro fondo es un supuesto fondo de neutrinos, y probablemente también debería haber un fondo de gravitones.
Estas partículas, en concreto el fondo de fotones, se encuentran en cualquier lugar del universo. Lo mismo debería ocurrir para el resto de los fondos.
En análisis de las ligeras inhomogeneidades del fondo de fotones ha proporcionado dos premios Nobel en 2006
En este blog encontrarás varias entradas sobre el fondo de microondas siguiendo la etiqueta de abajo.
La clave para entender la idea tras las estrellas de bosones es el principio de exclusión de Pauli y el concepto asociado de presión de degeneración.
El principio de exclusión de Pauli significa que dos fermiones no pueden estar en el mismo estado. El mismo estado significa mismos números cuánticos y misma posición. Es por ello por lo que dos electrones en el mismo orbital atómico, de los cuales existe cierta probabilidad de que estén en el mismo punto espacial, no pueden tener el mismo espín.
Relacionado con esto está en concepto de presión de degeneración. Si uno tiene un gas de fermiones, por ejemplo electrones, y lo comprime, aparece una presión dada por el principio de incertidumbre de Heisenberg. Este principio dice que dx dp > h, es decir, que la indeterminación simultanea del momento y la posición ha de ser siempre mayor que la constante de Planck. Siendo dp positivo, esto hace que a mayor confinamiento en la posición la indeterminación en el momento lineal de los fermiones es cada vez mayor, y con ello su momento lineal medio aumente.
En las estrellas enanas blancas la presión de degeneración de un gas de electrones es lo que las mantiene estables frente al colapso gravitatorio. Si la masa es mayor y el colapso más fuerte, los electrones acaban por ser confinados tanto que el principio de Pauli ya no puede cumplirse. Como este principio es extremadamente fundamental, la solución de la naturaleza a esta situación es convertir el gas de electrones en otra cosa, uniéndolos a los protones para dar lugar a neutrones.
Los neutrones, a su vez, también son fermiones y el principio de exclusión de Pauli se cumple para ellos. Otra vez, si la masa y el colapso gravitatorio son suficiéntemente fuertes, los neutrones acabarán por estar tan confinados que deberán convertirse en otra cosa a costa de mantener la validez del principio de exclusión de Pauli. El siguiente paso aquí es que, debido a las altísimas presiones, los quarks que componen a los neutrones pueden quedar libres (la interacción nuclear fuerte disminuye con la energía), dando lugar a una estrella de quarks.
En principio nada impide teóricamente que la gravitación sea aun más fuerte todavía. En general, hemos visto que la naturaleza procede de forma que convierte unos fermiones en otros con presión de degeneración mayor tan pronto que el principio de exclusión está en peligro de ser violado. El siguiente paso, a falta de partículas más fundamentales o posibles transformaciones más energéticas de los quarks, es ya la formación de un agujero negro en el cual la noción de fermión carece de sentido. En general, en el agujero negro las leyes físicas conocidas hoy no son válidas.
Ahora imaginemos la misma situación pero con bosones. Para ellos el principio de exclusión de Pauli no es válido. Dos bosones pueden estar perféctamente en el mismo estado y con ello en la misma posición. Si la gravitación de un gas de bosones es muy fuerte, éstos adquirirán una presión debido al principio de incertidumbre la cual podrá contrarrestar a la gravitación. Si la gravitación aumenta, los bosones adquirirán mayor presión debido al principio de incertidumbre. En principio, la presión que pueden adquirir es arbitrariamente grande. A diferencia de los fermiones, los bosones mantienen su identidad y todo se reduce a un equilibrio entre colapso y principio de incertidumbre.
El radio de una estrella así será no obstante extremadamente pequeño, de ahí la dificultad de diferenciarlas observacionalmente de los agujeros negros. Por otro lado, hay que notar que, al igual que los agujeros negros, las estrellas de neutrones tendrán discos de acreción de material interestelar. Estando compuesto este por fermiones, es de esperar que la estrella de bosones trague masa fermiónica, la cual empezará a ser dominante tarde o temprano, y acabe convertida también en un agujero negro.
La física de las estrellas de bosones es muy compleja y esto mencionado aquí es sólo una noción intuitiva. A mí me consta a que la objección de la acreción de material fermiónico mencionada en el párrafo anterior es bastante fuerte, y hace que la hipótesis quede algo de lado como alternativa a los agujeros negros centrales de galaxias. Aquí pongo un par de referencias diversas sobre el tema, el interesado puede buscar en google o en arXiv.org con "boson stars".
Lin Yutang. La importancia de vivir.
DEL SENTIDO DEL HUMOR
Dudo que haya sido plenamente apreciada la importancia del humor, o la posibilidad de su empleo para modificar la cualidad y el carácter de toda nuestra vida cultural: el papel del humor en la política, en el estudio y en la vida. Porque su función es química, mas que física, altura la textura básica de nuestro pensamiento y experiencia.
La incapacidad de reír le costó al ex Kaiser Guillermo un imperio. Guillermo de Hohenzollern podría reír probablemente en su vida privada, pero siempre parecía terriblemente impresionante con sus bigotes hacia arriba en la vida pública, como si estuviera furioso con alguien. Y luego la calidad de su risa y las cosas de que reía- risa por la victoria, por el buen éxito, por ponerse sobre los demás- fueron factores igualmente importantes para determinar la fortuna de su vida. Alemania perdió la guerra porque Guillermo de Hohenzollern no sabía en que punto reír. Sus sueños no estaban contenidos por la risa.
Por otra parte, la tremenda importancia del humor en la política solo puede ser comprendida cuando imaginemos un mundo de gobernantes bromistas. Enviemos por ejemplo, cinco o seis de los mejores humoristas del mundo a una conferencia internacional, y démosles poderes plenipotenciarios de autócratas, y el mundo se salvará. Como el humor marcha necesariamente de la mano con el buen sentido y el espíritu razonable, mas algunos poderes excepcionalmente sutiles de la mente para notar inconsistencias y locuras y mala lógica, y como esta es la forma mas alta de la inteligencia humana, podemos estar seguros de que cada nación estará representada en la conferencia por su espíritu mas cuerdo y mas sano.
Porque, ¿quiénes iniciaron nuestras guerras? Los ambiciosos, los capaces, los hábiles, los que alientan designios, los cautos, los sagaces, los altaneros, los patriotas en exceso, los inspirados por el deseo de “servir” a la humanidad, los que tienen que hacerse una “carrera” y6 causar una impresión en el mundo, que esperan poder mirar al mundo con los ojos de una figura de bronce montada sobre un caballo de bronce en alguna plaza. Es curioso que los capaces, los hábiles y los ambiciosos y altaneros, son al mismo tiempo los mas cobardes y confusos, pues carecen de la valentía y la profundidad y la sutileza de los humoristas. Están siempre dedicados a trivialidades, en tanto que los humoristas, con su mayor alcance de espíritu, pueden pensar en cosas mas grandes.
Esto es lo que concibo como función química del humor: cambiar el carácter de nuestros pensamientos. Creo en verdad, que llega a la raíz misma de la cultura, y abre un camino para llegar a la Edad Razonable en el mundo humano del futuro. Para la humanidad no puedo imaginar ideal mas grande que el de la Edad Razonable. Porque eso, al fin y al cabo, es la única cosa importante: la llegada de una raza de hombres imbuidos de un espíritu razonable mas grande, con mayor predominio del buen sentido, con pensamientos sencillos, un temperamento apacible y una perspectiva culta. El mundo ideal para la humanidad no será un mundo racional, ni un mundo perfecto en sentido alguno, sino un mundo en el que se perciban con certeza las imperfecciones y se resuelvan razonablemente las disputas.
Es difícil imaginar esta especie de nuevo mundo, porque nuestro mundo actual es tan diferente. En conjunto, nuestra vida es demasiado compleja, nuestros estudios demasiado serios, nuestra filosofía demasiado sombría y nuestros pensamientos y estudios hacen que el mundo presente sea hoy tan desagradable. Debe darse por sentado que la sencillez de la vida y de pensamiento es el ideal más alto y más cuerdo de la civilización y la cultura, que cuando una civilización pierde su sencillez y los sofisticados no abandonan su sofisticación, la civilización se perturba cada vez más y degenera. El hombre se convierte en esclavo de las ideas, pensamientos, ambiciones y sistemas sociales que son su producto. Pero los humoristas manejan las ideas y los pensamientos, como los campeones de golf o de billar manejan sus palos o tacos. Hay en ellos una facilidad, una seguridad, una ligereza de toque que proviene de la maestría. Al fin y al cabo, solo el que maneja ligeramente sus ideas es dueño de ellas. La seriedad , es a fin de cuentas, solo un signo de esfuerzo, y el esfuerzo es un signo de imperfecta maestría.
La sencillez es, pues, paradójicamente, el signo externo y el símbolo de la profundidad de pensamiento. Me parece que la sencillez es lo más difícil de lograr en el estudio y en la literatura. Muy difícil es la claridad de pensamiento, y sin embargo, sólo cuando el pensamiento se hace claro resulta posible la sencillez.
La expansión del universo es adiabática para todo volumen suficiéntemente grande. Esto es así porque para todo volumen suficiéntemente grande el principio cosmológico es aplicable, lo cual significa que no existen flujos de materia o energía a través del volumen mencionado. Por tanto, se puede aplicar la siguiente ecuación relacionando energía interna y presión de un gas:
La interpretación del trabajo 
es no obstante algo diferente de la de un gas en expansión adiabática en un volumen, donde el gas actúa con presión en las paredes del volumen. Aquí se trata más bien de un trabajo realizado en cada punto del espacio. Para un fluido perfecto, que en cosmología es asumido como modelo para los componentes del universo, se tiene 
y 
. Por tanto:
Esto se resuelve en:
^{-\omega})
Esto muestra que todo depende del parámetro de estado 
.
- Si
entonces la energía interna se conserva.
- Si es mayor que cero, entonces la energía interna disminuye a medida que el volumen aumenta. Este es el caso de gases relativistas, como el fondo cósmico de microondas, en el cual el aumento de la longitud de onda de los fotones contribuye a que estos pierdan energía al expandir.
- Si es menor que cero, entonces la energía interna aumenta. Este es el caso de la energía oscura. Si se trata de una constante cosmológica
, por lo que 
, y la densidad de energía se mantiene constante 
. pese a la expansión del espacio. Esto no significa que la conservación de la energía se viole, ya que hay que tener en cuenta que existe una presión, realizando un trabajo, que contribuye a tal comportamiento.
La misma ecuación mencionada arriba se puede obtener de la relatividad general calculando la divergencia del tensor de energía-momento en un espacio cosmológico. Estos resultados son exactos para un espacio-tiempo cosmológico y no dependen de ninguna aproximación. No obstante, está por ver el significado físico de ese trabajo realizado durante la expansión. Uno podría pensar que va a la expansión del espacio-tiempo, pero faltando una definición de energía del espacio-tiempo ese trabajo también puede considerarse como perdido. Esto nos pone frente a uno de los problemas conceptualmente más complicados en la relatividad general: la definición de energía y su conservación.
