Primero, hay que mencionar que el sol gira alrededor de el centro galáctico con un período de unos 230 millones de años a una velocidad de unos 220 km/s. Estos números no son conocidos con gran exactitud, pero para hacernos una idea bastarán (ver aquí y aquí para más información). Podemos considerar en primera aproximación, idealizada, que se trata de una órbita circular alrededor del centro de la galaxia.
Pero sabemos por un lado que las órbitas gravitatorias no son circulares en general sino elípticas. Por ejemplo, el movimiento de la tierra alrededor del sol es una órbita elíptica o kepleriana. No obstante, la galaxia no es un cuerpo central esférico sino una distribución de masa con simetría cilíndrica. Esto desvía ligéramente la órbita respecto de una órbita kepleriana. Por otra parte, el sol es gravitacionalmente influido por las estrellas cercanas a él. Todo en uno estas desviaciones del movimiento del sol respecto de la órbita circular ideal son pequeñas y el movimiento puede separarse razonablemente en dos partes (i) un movimiento de traslación circular en torno al centro galáctico y (ii) un movimiento peculiar debido a interacciones gravitacionales que lo desvían del movimiento circular. Definamos con precisión estos dos movimientos.
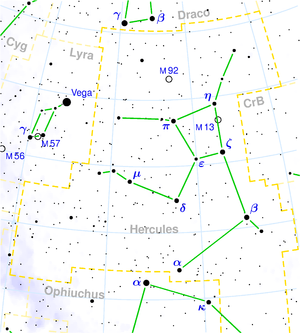
El Sistema de Reposo Local o Local Standard of Rest (LSR) en inglés es un marco de referencia que se encuentra en una órbita circular alrededor del centro galáctico. El movimiento del Sol con respecto a la dinámica del LSR se denomina movimiento peculiar o movimiento solar básico. Es de unos 16.6 km/s hacia AR = 17:49:58, Dec = 28:07:04. Este valor difiere de una referencia a otra, pero para nuestra precisión un valor de AR = 18:00:00, Dec = 28:00:00 será suficiente. Esta dirección, hacia la que el Sol se mueve con respecto al LSR, se denomina ápex. El ápex a AR = 17:49:58, Dec = 28:07:04 se encuentra en la constelación de Hércules en el cielo nocturno.
Los valores de AR (Ascensión Recta) y Rec (Declinación) son en coordenadas ecuatoriales, un tipo de coordenadas celestes muy usadas en astronomía que determinan la posición de un objeto en la esfera celeste respecto al ecuador celeste y al equinoccio vernal. Si esto te es desconocido conviene que visites la página de wikipedia sobre las coordenadas ecuatoriales.
El movimiento del sol respecto de las estrellas cercanas, dentro del LSR, se establece midiendo la velocidad radial de las estrellas en la vecindad solar. El resultado, por ejemplo, el valor dado anteriormente, depende de la profundidad de la muestra (el número de estrellas usado para la media), y las clases espectrales de las estrellas seleccionadas (que da lugar a mayor o menor dispersión de la muestra). Para evitar esta incertidumbre en esta definición tan importante, los astrónomos han definido un marco respecto del cual el movimiento solar es de 20 km/s hacia AR = 18:00:00.0, Dec = 30:00:00. Este marco se denomina LSR cinemático (kinematical LSR) y el movimiento del sol dentro del LSR cinemático se denomina movimiento solar estándar. Estríctamente el LSR mencionado anteriormente, respecto del cual el sol se mueve con unos 16,6 km/s hacia AR = 17:49:58, Dec = 28:07:04 se denomina LSR dinámico (dynamical LSR). A pesar de que el LSR cinemático es el más utilizado, vamos a olvidarnos de él y centrarnos en el LSR dinámico que es más intuitivo de entender.
Observemos la siguiente imagen:
Esto se supone que representa la mitad de la galaxia, con el núcleo galáctico y centro a la derecha. El LSR se mueve en una órbita circular alrededor del centro galáctico. Por otra parte, dentro de o respecto del LSR, en el recuadro pequeño, el sol tiene su propio movimiento peculiar con su velocidad peculiar. Para entender mejor el movimiento del LSR debemos echar un vistazo a las coordenadas galácticas. El siguiente dibujo da una idea de este sistema coordenado:

Estas coordenadas se definen de tal modo que la longitud LII = 90 apunta en la dirección de la rotación de la galaxia. La latitud BII = 0 corresponde con el plano galáctico. De este modo, el LSR se mueve hacia LII = 90, BII = 0. ¿Dónde está esa dirección ubicada en el cielo nocturno? Esta dirección corresponde en el cielo con la constelación del Cisne. Para comprobarlo podemos ir a esta página donde podemos convertir las coordenadas ecuatoriales de la constenación del Cisne (aprox AR = 20:62h, Dec =+42:00) a galácticas. Por medio de esta página podemos comprobar también la orientación de la eclíptica (el plano del movimiento de la tierra alrededor del sol) respecto del plano galáctico. Del dibujo de las coordenadas ecuatoriales en el enlace mencionado de wikipedia, vemos que la normal a la eclíptica se encuentra a AR: 16.00.00 y Dec: 66.5h. Insertando en la calculadora se tiene LII= 99.8 BII= 41.3, es decir, la normal apunta casi en la dirección del movimiento del sol.
Así llegamos a nuestro primer resultado: el sistema solar se mueve en órbita circular con el LSR hacia la constelación del Cisne, a una velocidad de unos 220 km/s y con la eclíptica orientada de forma casi perpendicular a su movimiento de traslación.

Además, hemos visto que el sistema solar se mueve dentro de o respecto del LSR hacia la constelación de Hércules con una velocidad de unos 20 km/s. Ahora queremos comparar las dos velocidades.
En primer lugar, es evidente que la peculiar velocidad del sol es pequeña si se compara con la velocidad circular (menos del 10%). En segundo lugar, nos gustaría saber la dirección del peculiar movimiento en coordenadas galácticas. Para ello tenemos que convertir las coordenadas ecuatoriales del ápex en coordenadas galácticas. Para ello volvemos a la página mencionada e insertamos AR = 18:00:00, Dec = 28:00:00, para obtener más o menos LII = 54.00 y BII = 23.00. Si observamos la figura anterior, teniendo en cuenta que LII = 90, BII = 0 es la dirección de movimiento del LSR, se puede ver que el movimiento peculiar del sol, LII = 54.00, BII = 23.00, tiene un componente en la misma dirección que el movimiento del LSR, otro componente hacia el centro galáctico y otro componente hacia el polo norte galáctico:
El movimiento vertical respecto del plano galáctico es interesante ya que el sol resulta tener un periodo de oscilación de varios millones de años respecto del plano galáctico. Este movimiento se ha especulado como causa de extinciones masivas, postulándose el paso por el plano galáctico como causa de perturbaciones de la nube de Oort y el consiguiente bombardeo del interior del sistema solar con cometas. El movimiento horizontal respecto del plano galáctico es consecuencia de la simetría cilíndrica de la galaxia, que hace que las órbitas deban ser modeladas por medio de epiciclos en general (más información por ejemplo en An Introduction to Modern Astrophysics, Carroll & Ostile).
Hemos situado las direcciones del movimiento del LSR y peculiar en el cielo y las hemos comparado, tanto en coordenadas ecuatoriales como galácticas. Ahora queremos saber cómo se mueve el sistema solar hacia el ápex ¿se mueven hacia arriba, hacia abajo, hacia la izquierda, hacia la derecha, etc? Evidentemente estos términos no tienen ningún significado en el espacio exterior, pero podemos preguntarnos con sentido sobre el movimiento del sistema solar respecto del plano de la eclíptica (el plano de la órbita terrestre alrededor del Sol).
Lo que queremos saber es el ángulo entre la dirección normal al plano de la eclíptica y la dirección el ápex. Sea R1 la dirección celeste del polo norte (Dec = 90:00:00). Sea R2 la dirección celeste hacia el ápex (AR = 18:00:00, Dec = 28:00:00). Sea R3 la dirección celeste de la normal a la eclíptica. Estos tres vectores cortan la esfera celeste en tres puntos que forman un triángulo esférico. Sabemos que el ángulo entre R1 y R2 es 90-28 = 62 grados. Sabemos que el ángulo entre R1 y R3 es igual a la inclinación de la eclíptica que son 23.5 grados.
Aplicando trigonometría esférica:
cos(R2 - R3) = cos(R1 - R3) cos(R1 - R2) + sin(R1 - R3) sin(R1 -R2)
(R2 - R3) = arccos [cos(23.5) cos(62) + sin(23.5) sin(62)] (R2 - R3) = 40
En definitiva, nuestro sistema solar se mueve hacia la constelación de Hércules con un ángulo de 40 grados respecto de la normal a la eclíptica:


3 comentarios:
Felicidades por el blog y gracias por el link. Sigo tus estimulantes posts.
Gracias. Un saludo.
Muy interesante y explicativo tu blog. Yo estoy estudiando astronomía (en la universidad) y ahora mismo tengo que realizar un trabajo sobre el módulo y dirección de la velocidad del sol en la galaxia usando las velocidades radiales de las estrellas cercanas.
Me ha servido mucho lo que escribiste para ir aclarando la idea, gracias!
Publicar un comentario