Tiempo inextenso, espacio extenso

(Editada el 5 de septiembre de 2008: addendum al final)

¿Por qué observamos el espacio con extensión pero el tiempo no? En esta entrada vamos a intentar una respuesta a tal pregunta aparentemente tan sencilla, cosa que además nos servirá de pretexto para tocar de refilón el tema de la causalidad en la relatividad.

Esta entrada es el resultado de una discusión en los foros de la web de física que tenía como intención una definición rigurosa de observar con extensión además de la diferenciación en este aspecto entre espacio y tiempo. No considero que la dada sea una explicación acabada del todo, y creo que aún se le podría sacar algo de partido a este tema o a esta pregunta aparentemente tan sencilla.

Empecemos con la causalidad en la relatividad. En la relatividad especial un evento sólo puede ser influido por eventos que se encuentran dentro de su cono de luz. Esto es una consecuencia de la velocidad finita de la luz, como velocidad máxima de propagación de efectos a partir de sus causas. Como su nombre indica el cono de luz tiene forma de cono con vértice en un evento determinado P (OBSERVER en el dibujo de abajo) como muestra el diagrama de abajo para el caso de dos dimensiones espaciales.



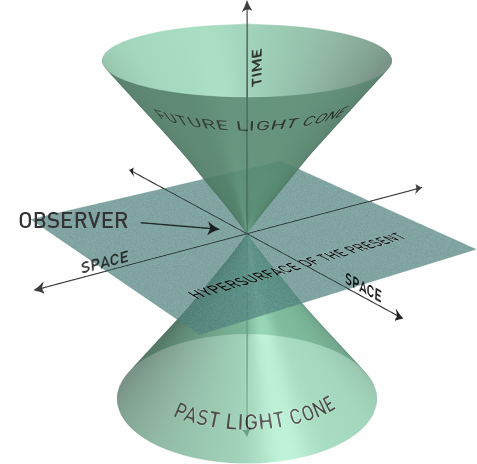
Un evento cualquiera es un punto en el espacio-tiempo que puede o no puede afectar a P. Si le afecta, es porque está dentro de su cono de luz. Le afectará en un instante determinado, pero no le afectará antes o más tarde, al tener el cono de luz forma de cono. La existencia de conos de luz da lugar a la posibilidad de ecuaciones diferenciales hiperbólicas que permiten formular problemas de valores iniciales bien definidos. Por ejemplo, la ecuación de onda. La solución en un punto determinado P a la ecuación de onda depende de los puntos dentro del cono de luz de P. Los puntos exteriores al cono de luz de P no afectan la forma de la solución de la función de onda en P.

Esta observación quizás trivial viene mejor ilustrada considerando en analogía un espacio en el cual los conos de luz no existen. Por ejemplo, el espacio euclídeo sin tiempo. En él las ecuaciones diferenciales son elípticas, como por ejemplo la ecuación de Laplace. En la ecuación de Laplace una solución en un punto determinado viene determinada por los valores de la solución en cualquier esfera con centro en ese punto. Esto es una consecuencia del conocido teorema de Gauss. Si definiesemos un punto en ese espacio como evento, todos los eventos de ese espacio afectarían a todos los eventos, constantemente y siempre.

Por otro lado, conviene notar cómo se comportan los conos de luz en un supuesto espacio en el cual la velocidad de la luz es infinita. En tal caso la generatiz del cono está inclinada noventa grados respecto del eje temporal y es paralela a los ejes espaciales. Esto significa que un evento P es afectado simultaneamente por todos los eventos localizados a un tiempo constante, o, equivalentemente, en la misma sección espacial del espacio-tiempo. Esta es la aproximación newtoniana que se aplica en nuestra vida cotidiana.

La relación de la noción de cono de luz con la de predictabilidad es digna de mención. En general, una definición de simultaneidad distante debe especificar los puntos del espacio-tiempo que se encuentran en una misma sección espacial (véase esto y esto). Los espacio-tiempos causalmente bien definidos son tales que contiene una sección espacial en la que se pueden definir las condiciones iniciales de todo problema de valor inicial que cubra todo el espacio-tiempo. Esto es la definición de superficie de Cauchy. Equivalentemente una superficie de Cauchy es una sección del espacio-tiempo por la cual pasa de un lado a otro de la superficie toda curva temporal una y sólo una vez. La figura siguiente muestra una superficie de Cauchy, que es, por ejemplo, el plano paralelo a xy, donde se encuentra el punto P. Si no hay curvas temporales cerradas todas las curvas temporales de los puntos en el espacio-tiempo (aquí: espacio de dos dimensiones y espacio-tiempo de tres) pasan una y sólo una vez por la superficie de Cauchy (el plano de dos dimensiones paralelo a xy). Existen otras superficies de Cauchy, de hecho existen infinitas, por ejemplo el mismo plano xy.



Vemos en la figura de arriba que para curvas temporales normalitas podemos definir superficies de x constante o y constante que sean cortadas dos veces por las curvas, sin que con ello peligre la causalidad. Pero las superficies de tiempo constante no pueden ser cortadas dos veces por la misma curva temporal. La definición de un problema de valores iniciales bien definido necesita por tanto de una clara diferenciación o asimetría entre espacio y tiempo. Los espacios con conos de luz como el de la relatividad especial tienen esta característica (relacionada por otro lado claramente con la signatura de la métrica). La especificación de los valores iniciales para cualquier evolución temporal bien definida debe ser realizada en una sección espacial del espacio-tiempo.

Lo que queremos explicar no obstante es una característica que es más bien observacional: el espacio lo consideramos o vemos como extenso, pero el tiempo usualmente no. En mi opinión la observación en extenso de algo es una consecuencia de la velocidad tan grande de la luz a efectos cotidianos. Es decir, observar algo con extensión sería sólo una apariencia, resultado de que nos veamos cotidianamente inmersos en un mundo gobernado por la mecánica newtoniana. Para poder precisar esto necesitamos una definición de lo que entendemos por considerar o observar algo extenso.

Consideremos la siguiente definición de observar algo en extenso:

Observo algo con extensión si observo simultaneamente sus extremos.

Esto es posible para un segmento espacial, ya que la luz se mueve en la horizontal en la aproximación newtoniana. Sin embargo, es imposible para un intervalo temporal, precisamente porque la luz se mueve en la horizontal. Esta definición refleja el hecho que podamos observar lo espacial como extenso y que lo temporal nos parezca inextenso.

La explicación también parece ser consistente con la interpretación usual que sólo existe el presente y el pasado y futuro no existen. Esta interpretación o ontología de la teoría es sin duda aplicable en la mecánica newtoniana, pero puede ponerse en duda en un marco de la relatividad especial, en la cual el pasado de alguien puede ser presente de otro debido a la relatividad de la simultaneidad.

En un marco relativista la situación es diferente. Un observador para el cual la luz se moviese muy despacio ¿observaría también el espacio con extensión y el tiempo sin extensión? Imaginemos las dos siguientes situaciones. Ambas por un lado en un marco de la relatividad especial con una velocidad finita de la luz, y, por otro en un marco de la mecánica newtoniana con una velocidad infinita de la luz. Las situaciones pretenden describir una situación análoga para el eje temporal y para el eje espacial en un espacio-tiempo de dos dimensiones. En todas las situaciones nosotros estamos localizados en x = 0.

Primero, dos extremos espaciales de algo A y B.

Para el caso newtoniano recibimos luz de sus extremos simultaneamente:


Diferentes extremos espaciales en la apoximación newtoniana

Para el caso con velocidad finita de la luz recibimos luz de sus extremos en dos instantes diferentes de tiempo:


Diferentes extremos espaciales en la relatividad especial

Segundo, una duración temporal de algo con extremos temporales 1 y 2.

Para el caso newtoniano recibimos luz de sus extremos instantaneamente para el instante 1 y luego para el 2:


Diferentes extremos temporales en la apoximación newtoniana

Para el caso con velocidad finita de la luz recibimos luz de sus extremos en dos instantes diferentes de tiempo:


Diferentes extremos temporales en la relatividad especial

Desde el punto de vista relativista la situación es algo sorprendente, porque la situación es simétrica desde el punto de vista observacional para el eje temporal y para el espacial. No obstante, algo hay que nos permite identificar A y B con los extremos de, por ejemplo, una barra, o en definitiva un objeto que existe a lo largo del tiempo, pero, sin embargo, nada nos permite identificar 1 y 2 como los extremos temporales de algo que existe a lo largo del espacio. Por ejemplo en x = 0 podemos decir que estamos escuchando los diez segundos que dura el sonido de nuestro reloj para despertarnos, pero el mismo sonido a cierta distancia de nosotros no es "el mismo", sino otro al provenir de otro reloj diferente que está alejado.

En el caso newtoniano parece más claro que podamos identificar A y B con los extremos de una barra y no podamos identificar 1 y 2 como los extremos temporales de algo que existe a lo largo del espacio. La observación de los extremos A y B es simultanea para nosotros, cosa que nunca puede ocurrir con 1 y 2. Esto se ajusta bien a la definición de observar con extensión dada. Adicionalmente, el hecho que todo fluya en el tiempo irremediablemente en una dirección da lugar a la situación que tras observar 2 nunca podamos volver a observar 1 otra vez. En el caso relativista este hecho no cambia prácticamente las cosas, ya que al igual que podemos recibir luz desde diferentes valores de t proveniente de A y B, podemos recibir luz desde diferentes valores de x proveniente de 1 y 2.

Para finalizar mencionar que esto, especialmente la definición dada, es una interpretación mía y con mucho gusto la discutiré con quien quiera ponerla en duda.



Addendum 5 de septiembre de 2008:

A veces las cosas son más sencillas de lo que parecen. Creo que el rollo anterior no viene al caso y es completamente prescindible. La razón de que observamos al tiempo inextenso y al espacio extenso está realmente en que todo fluye en el tiempo en una misma dirección.

Las reflexiones que hice antes en este tema son relacionadas de alguna forma con la noción de extensión espacial, pero creo que fallé en identificar ese punto como el esencial. Creo que hay una forma muy sencilla de entender la relación del paso del tiempo con su inextensión.

Como definición de observar algo con extensión tomaré la misma que tomé antes: observo algo con extensión si observo simultaneamente sus extremos. En un diagrama de espacio-tiempo para una dimensión espacial tal cosa puede representarse así:



Las líneas a trazos son rayos de luz que provienen de los extremos de algo que se encuentra en t = 0 y que observamos simultaneamente más tarde. Ahora bien - y esto creo que es una observación lamentablemente sencilla que no veo cómo no se me ocurrió antes - para que la misma cosa sea posible con el tiempo, debería ocurrir que:



Es decir, la luz (el rayo de arriba) debería viajar hacia atrás en el tiempo o fluir en contra de los demás objetos que van siempre hacia valores de t mayores.