La longitud de onda de de-Broglie

Hablemos sobre la longitud de onda de de-Broglie, en concreto de la existencia de tal longitud de onda para objetos macroscópicos. Aviso de entrada que lo que sigue es mi opinión personal. Aunque creo que está bien justificada, debo advertir que con ella me enfrento aparentemente contra miles de referencias en las que se afirma que la longitud de onda de de-Broglie para objetos macroscópicos existe, pero que es muy pequeña e indetectable. Yo dudo muy firmemente de tal cosa, aunque no descarto que haya algo que se me escapa en este asunto.

Leemos aquí y allá sobre la longitud de onda de la onda de probabilidad asociada a una pelota, a una persona, etc. No obstante, para poder afirmar esto hay que partir de la hipótesis que un objeto macroscópico tiene asociado una onda de probabilidad con su longitud de onda determinada. Veamos qué condiciones hay que plantear para aceptar tal situación.

En principio, la longitud de onda de la onda asociada tiene completo sentido para soluciones sinusoidales de la ecuación de Schrödinger. Para objetos más complejos, aunque no necesariamente macroscópicos, van a ocurrir dos cosas que creo ponen en cuestión este cuadro simplificado.

• Primera, si el objeto está en un estado puro, en general van a ser superposición de muchas diferentes longitudes de onda, por lo que hay que ser cuidadosos al hablar de esa única longitud de onda asociada.


• Segunda, el objeto puede estar en un estado mezclado. La ecuación de Schódinger, de la cual se deriva la relación de de-Broglie, describe la evolución temporal de estados puros. Por contra, un objeto macroscópico es un estado mezclado descrito por una matriz de densidad que no va a ser reducible a una función de onda, la cual a su vez tiene una evolución temporal diferente.

En general, los estados de un sistema se pueden clasifican en dos tipos, los estados puros y los estados mezclados. Los estados puros son estados de superposición cuántica y los estados mezclados son estados de desconocimiento. En los estados puros existen varios estados posibles sobre los cuales el sistema está en superposición. Según la cuántica esta superposición no tiene que ver con desconocimiento, sino que es un fenómeno básico de la naturaleza. Veamos especialmente el segundo punto de los de arriba con detalle tras mencionar cómo salvar el primero.

En el primer caso el objeto tiene una onda asociada al cumplir la ecuación de Schrödinger. No obstante, esta es superposición compleja de ondas planas. Para salir al paso podemos usar un elegante truco que se me ha mencionado en este hilo del foro de la web de física. Podemos utilizar el concepto de centro de masas. El valor esperado del momento del centro de masas nos permite definir una única longitud de onda a través de la relación de de-Broglie.

En el segundo caso las cosas cambian.

Los estados mezclados necesitan de una matriz de densidad 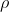para ser descritos, la cual a su vez no reducible a una función de onda. Este hecho hace que su evolución temporal no cumpla la ecuación de Schrödinger sino en general 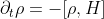. Y de ahí no es extraíble una onda asociada. Al menos a mí no me es conocida una forma de asignar una onda asociada a estados mezclados en general, cosa que veo respaldada por el experimento que voy a mencionar abajo.

El hecho de que un objeto esté en un estado mezclado se puede deber a dos razones: (a) entrelazamiento (b) desconocimiento. Estas son las dos razones que dan lugar a estados mezclados. Dejemos primerdo de lado la opción (b) y concentrémonos primero en la (a).

El entrelazamiento es una propiedad muy especial. Los estados entrelazados son puros, pero los subsistemas dentro de estados entrelazados son mezclados. En parte esto se puede entender en términos de pérdida de información: los estados mezclados suponen una falta de información para el que los considera, mientras que los puros no. Cuando hay entrelazamiento y nos preguntamos sólo sobre un subsistema resulta haber información faltante, ya que existen correlaciones con el otro subsistema que quedan "fuera" del subsistema en consideración. Esta falta de información es natural en subsistemas de sistemas entrelazados, ya que, por definición, los subsistemas de un sistema enrelazado son imposibles de separar debido a una correlación cuántica fuerte entre ellos. Esto lo muestro en mi página sobre la decoherencia, pero lo vamos a ver aquí mencionando un conocido experimento.

Imaginemos una fuente que emite partículas de momento lineal antiparalelo en dos direcciones diferentes 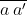y 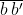. Digamos que 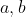están a la derecha y 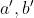a la izquierda.



Esto es, si en la derecha se encuentra una partícula en , entonces la partícula correspondiente en la izquierda debe encontrarse en 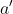y si en la derecha se encuentra la partícula en 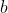, entonces la partícula correspondiente debe encontrarse en 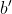. Para tales pares entrelazados se tiene:



Este estado total es un estado puro y entrelazado (esto se ve notando que no es posible factorizar en los estados de las partículas individuales). Para una sola de las partículas - por ejemplo la que se mueve hacia la derecha, que no tiene prima - no obstante se trata de un estado mezclado. Es decir, no existe una sola función de onda para una de las partículas que cumpla la ecuación de Schrödinger. Al ser un estado mezclado los estados básicos 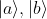cumplen la ecuación de Schrödinger, pero no el estado mezclado resultante de ambos. La ecuación de Schrödinger es válida para el estado total entrelazado que es puro, pero no para un subsistema del estado entrelazado que es mezclado. Para mostrar que se trata de un estado mezclado refiero a mi página sobre la decoherencia o a Wikipedia que también explica con un ejemplo sencillo cómo los subestados de estados entrelazados son todos mezclados.

En definitiva, las partículas generadas así no pueden crear interferencia en un experimento de doble ranura (por ejemplo, todas las lanzadas hacia la derecha). Esto es debido a que su estado no es puro. Este experimento ha sido realizado ya y está descrito por ejemplo en Experiment and the foundations of quantum physics de Anton Zeilinger. Podemos por tanto asignar un momento a tal partícula, el que resulta de calcular el valor esperado más probable del momento de la partícula. Pero no podemos asignar luego una onda asociada al momento con su longitud de onda.

Fijémonos en la diferencia con la partícula libre y no entrelazada. En tal caso también tenemos un valor esperado del momento (está en un autoestado de momento), sin embargo sí decir que a tal momento asociamos una onda plana solución de la ecuación de Schrödinger. Esta onda plana describe completamente y de forma correcta a la partícula libre y no entrelazada. La partícula libre y no entrelazada presenta inteferencia cuando es lanzada contra una doble rendija (cuando son lanzadas muchas idénticas). Por contra, las partículas entrelazadas no la presentan. En mi opinión estamos obligados a concluir que en este segundo caso la asociación con un fenómeno ondulatorio de probabilidades no es correcta.

He mencionado antes que existen dos razones para tener estados mezclados: (a) entrelazamiento (b) desconocimiento. La cuestión ahora qué ocurre con los objetos macroscópicos. En principio yo asumo que ambas razones son relevantes. Por ejemplo, la radiación térmica de cualquier objeto macroscópico debería estar entrelazada con este. Ahora bien, uno puede cuestionarse - al menos yo con mi conocimiento parcial del tema - si para objetos macroscópicos el entrelazamiento es relevante. Quizás tal fenómeno es despreciable.

No obstante, lo que está claro es que un objeto macroscópico es un macroestado, es decir, una clase de equivalencia de muchos microestados. No conocemos las funciones de onda de las partículas y esto es precisamente una propiedad que define a lo que comúnmente denominamos mundo macroscópico. El objeto está en un estado mezclado, descrito por una matriz de densidad, donde aparecen factores de probabilidad debido al desconocimiento, y no por una función de onda.

La cuestión ahora es si el argumento previamente presentado sobre la imposibilidad de asignar una onda asociada a un estado mezclado sigue siendo válido para el caso de estados mezclados por desconocimiento. En el formalismo yo no veo cómo asignar ondas asociadas a estados que no cumplen la ecuación de Schrödinger. La cuestión es si describir a un estado macroscópico como mezclado debido al desconocimiento es sólo una forma de ver las cosas y si de igual forma podría habérselo descrito como un estado puro si se conociese perféctamente. Y con esto entramos ya en un terreno muy difícil: ¿es un macroestado sólo un artilugio de nuestra descripción, parcial, o algo genuínamente real? ¿es la entropía algo real? ¿aumentaría la entropía del universo si conociesemos perféctamente la función de onda de todas sus partículas? etc.

Resumen: un tema para pensar y debatir mucho.

El sombrero dorado de Schifferstadt

A las puertas de la Selva Negra y al sur de la maravillosa región vinícola de la Mosela en Alemania se encuentra la cuidad de Schifferstadt. A las afueras de Schifferstadt un campesino encontró un sombrero dorado enterrado en el campo en el que trabajaba un 29 de abril de 1835. Fué el primero de cuatro sombreros de oro encontrados en Alemania y Francia. Tras el sobrero de Schifferstadt vinieron el sombrero de d'Avanton en 1844, el de Ezelsdorf-Buch en 1953 y más recientemente el conocido como sombrero dorado de Berlín.



El sombrero dorado de Schifferstadt data de los siglos diecinueve o veinte antes de Cristo. A los sombreros se los considera un símbolo religioso usado por los sacerdotes de una a finales de la Edad de Bronce en Europa Central. El culto al sol estaba entonces muy extendido en Europa Central. Tres de los cuatro sombreros tienen un pedestal como ampliación en la parte inferior del cono y sus aberturas son ovaladas (no redondas), con diámetros y formas más o menos equivalentes a las de un cráneo humano.

La representación figural de un objeto parecido a un sombrero cónico sobre una losa de piedra de la tumba del Rey en el pueblo de Kivik, en el sur de Suecia, apoya firmemente su asociación con la religión y de culto, así como el hecho de que los conocidos ejemplos parecen haber sido depositados (enterrados) cuidadosamente (véase wikipedia).



Esta conexión con escandinavia la muestra también la relación con el culto al sol que muestra el carro de Trundholm:



Lo espectacular de los sombreros de oro es que en diferentes alturas tienen marcas que permiten la determinación de calendarios y la conversión entre ellos. No necesariamente fueron usados como tales, pero sí parece claro que al menos reflejan los conocimientos de la época, quizás sólo como adorno.

En esta entrada en este blog: Glaubendorf 2 y el orígen de la astronomía en Europa reflexionaba sobre los conocimientos astronómicos de los antiguos pobladores europeos quizás plasmados en los círculos existentes en el centro de Europa. Tanto los sombreros de oro como el disco celeste de Nebra muestran que los conocimientos astronómicos entre los europeos eran considerables en el segundo milenio antes de Cristo. Está por ver en qué medida parte de estos conocimientos estaban existentes ya varios milenios antes. Los círculos en el centro de Europa son un indicio de ello, aunque pruebas definitivas con descripciones detalladas evidentamente faltan.

En cualquier caso es bonito ver como estos objetos - los círculos, los sombreros dorados, el disco de Nebra - nos marcan el inicio en la línea del desarrollo del conocimiento astronómico. La historia está viva en nosotros mismos y esos objetos son en definitiva un instrumento para conocernos mejor y aprender a valorar nuestro pasado.

Desastre con el LaTeX

El servidor de LaTeX de www.forkosh.dreamhost.com impide el uso de LaTeX enlazando desde fuera:



En este blog he escrito muchas entradas haciendo uso de este servidor, por lo que ahora va a haber muchas que quedan illegibles, sin las fórmulas correspondientes. Una solución es pasar todo el blog a wordpress.com, que tiene servidor con LaTeX propio. Antes de tomar tal drástica medida voy a empezar a hacer uso externo de www.codecogs.com:



E iré corrigiendo las entradas antiguas. Esta es una medida que vuelve a ser una trampa en definitiva, por lo que quizás no está de más pensar seriamente en el traslado a wordpress.com. Un fastidio.

El coche y el garaje

La clásica paradoja del coche y el garaje, conocida en inglés como "the barn and the pole" o similares, es explicada muchas veces con diagramas espacio-temporales. Aquí una explicación con números, que pretende ser lo más sencilla posible.

Tenemos un coche de longitud (en las unidades que sea) y un garaje de longitud . El garaje tiene una puerta de entrada a su principio (en y a su final una puerta de salida (en ). El coche se mueve a velocidad relativista con en 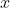hacia el garaje. Esto corresponde con una velocidad y es elegida así para simplificar luego los cálculos.

Desde el punto de vista del garaje

La situación es simple. La longitud del coche medida en el sistema de referencia estacionario con el garaje es:



Esta es la contracción de Lorentz. Por tanto, desde el punto de vista del garaje, el coche va a caber dentro del garaje. Para comprobar la veracidad de la contracción de Lorentz, alguien dedice capturar el coche de la siguiente forma.

Las puertas del garaje quedan ambas abiertas hasta que el coche está dentro. En el momento en el que el coche queda dentro, ambas puertas se cierran sólo un instante y luego se vuelven a abrir. La puerta de salida se cierra cuando la parte trasera del coche llega a y la puerta de entrara se cierra cuando la parte trasera del coche sobrepasa .

Inmediatamente después que se dan estas condiciones, ambas puertas se abren otra vez. El coche, sin cambiar en ningún momento su velocidad, queda capturado un instante en el garaje y luego sigue, pasando de largo hacia mayores de .

Desde el punto de vista del coche

La longitud del garaje medida en el sistema de referencia comóvil con el coche es:



Aparentemente el garaje es demasiado pequeño para que quepa el coche, pero ahora veremos que la relatividad de la simultaneidad sale al rescate. Supongamos que el coche entra en el garaje.

Sea el intervalo de tiempo entre los eventos (A) llegada de la parte frontal del coche a la pared final del garaje y (B) llegada de la parte trasera del coche a la puerta de entrada al garaje.

Medido en el sistema de referencia estacionario respecto del garaje estos dos eventos A y B son simultaneos . Medidos en el sistema de referencia comóvil con el coche:



Esta es la transformación de coordenadas de acuerdo con las transformaciones de Lorentz. Prima son cantidades en el sistema del coche y sin-prima en el sistema del garaje.

es la separación espacial entre ambos eventos A y B, medida en el sistema del garaje, es decir, la longitud del coche medida en el sistema del garaje: . El intervalo corresponde con la separación temporal entre los eventos, medido en el sistema del garaje, que vimos que es cero. Por tanto:



Esto significa que los eventos A y B no son simultaneos en el sistema comóvil con el coche. Cuando la parte frontal del coche llega al final del garaje (evento A) y la puerta de salida se cierra, el observador en el sistema comóvil con el coche ve que hay tiempo todavía hasta que la puerta de entrada se cierre. Si durante ese tiempo la parte trasera del coche se mueve con velocidad , el coche podrá meter todavía una longitud



dentro del garaje. Como la longitud del garaje es medido desde el coche, y el coche mide medido en el coche, ocurre que una vez el coche dentro del garaje quedan de coche fuera (todo esto medido en el coche). Precisamente estos que quedan fuera pueden ser metidos aún debido a que el cierre de puertas no es simultaneo.

El Cosmos y el misterio

El Cosmos es todo lo que es o lo que podrá ser. Nuestras más ligeras contemplaciones del cosmos nos hacen estremecer - sentimos como un cosquilleo nos llena los nervios, una voz muda, una ligera sensación como en un recuerdo lejano o como si cayéramos desde la altura. Sabemos que nos aproximamos al más grande de los misterios. Cosmos. Carl Sagan.

El día 13 de diciembre de 1985 recibí como regalo el libro Cosmos de Carl Sagan. Recuerdo el día y recuerdo la magnífica sensación al leerlo, entendiendo poco, pero maravillado con las palabras de Sagan y las fotos y dibujos en el libro. Desde entonces habre leído pasajes en él hasta mil veces, y siempre me vuelve a gustar. Cosmos es sin duda el libro entre libros para toda una generación de amantes del universo que ha determinado el destino de aficciones y profesiones de muchos.

La física es bella por la relación con las matemáticas, y es bella por la sencillez de sus principios. Pero exste otro tipo de belleza más profunda, no intelectual. Es lo que nos hace sentir esa voz muda o el nudo en el estómago cada vez que admiramos cómo el universo oculta y codifica sus secretos más valiosos en un lenguaje que empezamos a entender. En esta época tendemos a valorar quizás excesivamente lo que sabemos, y queremos encontrar rápidamente explicaciones completas y unificadoras, cuando lo más humano en la física es precisamente el misterio de lo desconocido. La capacidad de formular rigurosamente preguntas adecuadas que son actuales tras una y otra generación, y sobre las cuales encontramos atisbos de respuestas.

Precisamente eso, el misterio de un universo increible, es lo que más me atrae de ella. Muchos científicos han intentado transmitir esta sensación, como Albert Einstein por ejemplo en EL SENTIMIENTO CÓSMICO RELIGIOSO, o ver la bonita entrada: Einstein y belleza en el blog de José Ignacio Latorre. Pero ha sido Carl Sagan el que ha sabido plasmar esto como ningún otro para la generación que ha tenido la suerte de verle en la televisión y leerle luego. Cuanto más sabemos sobre el universo, más podemos maravillarnos y sorprendernos de su naturaleza. Parafraseando a John Archibald Wheeler en una metáfora que proviene de Huxley:

We live on an island surrounded by a sea of ignorance. As our island of knowledge grows, so does the shore of our ignorance.

Qué bello es estar en la orilla y mirar hacia el horizonte.


Carl Sagan

Mitos y leyendas: la radiación de Hawking

Vamos a ver en este artículo una explicación detallada de la radiación de Hawking, más allá de las explicaciones populares en la red.

La explicación usual

Nos dice el artículo de wikipedia:

Una de las consecuencias del principio de incertidumbre de Heisenberg son las fluctuaciones cuánticas del vacío. Estas consisten en la creación, durante brevísimos instantes, de pares partícula-antipartícula a partir del vacío. Tales pares se desintegran rápidamente entre sí devolviendo la energía prestada para su formación. Sin embargo, en el límite del horizonte de sucesos de un agujero negro, la probabilidad de que un miembro del par se forme en el interior y el otro en el exterior no es nula, por lo que uno de los componentes del par podría escapar del agujero negro.

Es decir, algo así:


En la explicación heurística el horizonte impide la aniquilación de un par creado en el vacío por el principio de incertidumbre.

Esta es la explicación usual heurística de la radiación de Hawking, que uno encuentra en la mayoría de las páginas de la red. No obstante, esta explicación dista bastante de la realidad teórica y lleva a malentendidos. Veamos un par de conceptos que pretenden aclarar la situación, o al menos proporcionar una idea más cercana a la teoría.

Las partículas virtuales

Las partículas virtuales son un concepto que da lugar a muchas confusiones, especialmente a nivel de divulgación. Aparecen de forma natural en la teoría cuántica de campos cuando se estudian las interacciones. Consideremos por ejemplo la interacción electromagnética. La teoría cuántica de campos nos dice que toda interacción viene descrita por lo que se denomina vértices. Estos son puntos de interacción entre uno o varios campos. Estos vértices vienen determinados por diferentes exigencias que se imponen a la teoría, usualmente debido a condiciones de simetría.

El vértice para el electromagnetismo es uno único y consiste de dos elementos de partícula cargada y uno de fotón. Esto son tres elementos o tres líneas en un diagrama:


El vértice electromagnético.

El fotón es la línea ondulada. Las dos líneas gruesas representan una partícula antes y después de la interacción. Por tanto, si interactúan dos partículas cargadas sin emisión de radiación electromagnética (fotones) la línea del fotón debe mantenerse interna:


Interacción electrostática entre dos partículas cargadas, en la aproximación más simple que describe tal interacción.

Pues bien, todas las líneas internas de este tipo en los diagramas son partículas virtuales. Las líneas con extremos abiertos son partículas reales, que acaban en el detector de la colisión o se propagan libremente por el espacio. Al no haber líneas onduladas con extremos abiertos se trata de una interacción sin emisión de radiación electromagnética. El fotón en el diagrama sólo transporta una interacción y no es detectable, de ahí su nombre "virtual".

No hay otra forma mas que el diagrama de arriba de hacer que dos partículas cargadas, reales y de líneas con extremos abiertos, interaccionen por medio del vértice electromagnético. Bueno, realmente sí la hay, pero a costa de incrementar la complejidad:


Interacción electrostática entre dos partículas cargadas, describiendo tal interacción con mayor precisión.

Aquí se ve bien que las condiciones experimentales son las mismas: dos partículas cargadas - líneas de extremos abiertos - interactúan entre sí. La forma de la interacción es la electromagnética: el mismo vértice siempre con dos líneas gruesas y una ondulada, aunque repitiéndose varias veces. Se ve bien en los diagramas que se puede incrementar la complejidad pero siempre manteniendo dos condiciones: (1) siempre debe haber cuatro extremos abiertos (pasado y futuro respectivamente de las dos partículas cargadas) y (2) en cualquier intersección de líneas debe haber dos líneas gruesas y una ondulada, es decir, el vértice es siempre el electromagnético.

El incremento de complejidad también hace aparecer aquí partículas virtuales diferentes de fotones: hay líneas internas gruesas que corresponden por ejemplo con electrones y positrones virtuales. Con esto también queda clara otra cosa: sin interacciones - sin vértices - no hay partículas virtuales.

Entropía y osciladores armónicos

Las ondas en un estanque son ondas de entropía muy alta. Las moléculas del agua están en movimiento caótico y sus oscilaciones no siguen ninguna pauta determinada a nivel microscópico, salvo que se unen para dar lugar a una onda macroscópica. Por contra, las vibraciones en un sólido cristalino a muy baja temperatura tienen lugar en un entorno de entropía baja. Existe una red cristalina con átomos localizados, los cuales no cambian sus posiciones. Una perturbación en la posición de uno se propaga por la red, pero lo hace manteniendo la estructura.


Las ondas en el agua se produce en un entorno de alta entropía, que desplazan caóticamente a las moléculas en el líquido.

Este tipo de ondas, que tienen lugar en entornos de entropía muy baja, son ondas cuantizadas, es decir, con cuantos energéticos. En el caso de las vibraciones en sólidos a estos cuantos se los denomina fonones. El hecho que en el agua del estanque no se presenten ondas cuantizadas reside precisamente en el diferente nivel de entropía. Los sólidos cristalinos se modelan usualmente asumiendo que en cada punto de la red existe un oscilador armónico. El oscilador armónico es uno de los sistemas más generales de la física y consiste en algo que es desplazado de su posición de equilibrio una mínima cantidad y que es llevado hacia el equilibrio después por una fuerza de restauración, todo ello dando lugar a un característico movimiento sinusoidal a una determinada frecuencia fija. El el caso del sólido la perturbación es algo externo y la fuerza de restauración son las fuerzas moleculares que hacen que los átomos se mantengan en sus posiciones.


Las ondas en un sólido a baja temperatura sólo mantienen la escturctura y se dan en un entorno de baja entropía.

El oscilador armónico es un sistema interesante desde el punto de vista de la mecánica cuántica. En el estado de reposo clásico el oscilador armónico, o un oscilador armónico clásico por ejemplo de un objeto macroscópico enganchado a un muelle, está quieto y en su punto de reposo. Si consideramos un sistema cuántico que sigue las leyes del oscilador armónico (un átomo o una partícula ligada a alguna fuerza por ejemplo), en su estado de reposo no puede tener energía nula. Esto es así por el principio de incertidumbre, que impide al sistema tener una posición y un momento ambos determinados. El oscilador armónico cuántico tendrá por tanto siempre una mínima energía o momento diferente de cero. A este estado se lo denomina estado fundamental. La energía en el estado fundamental de un oscilador armónico es 1/2 h f, siendo h la constante de Planck y f la frecuencia de las posibles de oscilaciones del oscilador (cuando se pone a oscilar).


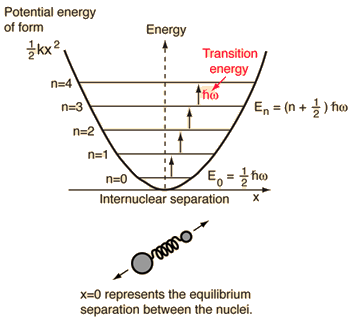
Niveles de energía del oscilador armónico cuántico para los átomos en una molécula.

La idea de campo y la energía del vacío

Esta introducción sirve para pasar a la teoría cuántica de campos, ya que en la teoría cuántica de campos los campos quedan descritos por una colección de osciladores armónicos. (En la teoría cuántica de campos, el campo es la noción fundamental de la que se derivan las partículas como excitaciones de este.) Es similar a la red cristalina, pero aquí es más extraño: hay una cantidad infinita de osciladores armónicos en cada punto del espacio. En un punto dado hay un oscilador por cada longitud de onda posible a la que el campo puede oscilar. Si hay un oscilador en un punto determinado está oscilando lejos de su estado fundamental, es decir oscilando a una determinada frecuencia, se dice que existe una exictación del campo dando lugar a una o varias partículas de esa longitud de onda (o momento lineal según la relación de de-Broglie). Cuando no existen partículas en todo el espacio los osciladores están inactivos y en su estado fundamental. Se dice igualmente que el campo está en su estado fundamental o vacío.

En la teoría cuántica de campos la energía de vacío del campo viene creada por el estado fundamental de todos los osciladores. Tenemos por tanto una cantidad infinita de contribuciones a la energía del vacío en cada punto (densidad de energía de vacío), una por cada 1/2 h f para todas las f, pese a que los osciladores no están activos. Este estado vacío es igual para todo sistema de referencia inercial. Esto significa que si yo estoy en un sistema inercial y tú también lo estás, y estamos tú y yo midiendo un determinado campo en una región del espacio, coincidiremos ambos en decir que el campo está en su estado fundamental y que, por tanto, no hay partículas y todos esos osciladores están inactivos. Esto es parte de la forma en la que una onda sinusoidal (movimiento del oscilador) transforma frente a transformaciones inerciales: cambia su frecuencia y da lugar a un efecto Doppler. Pero al ser la energía del vacío o el vacío mismo una suma sobre todas las frecuencias posibles, tal efecto es irrelevante ya que todas las frencuencias se desplazan una misma cantidad - y en un rango infinito tal cosa no se nota. Aprovecho para hacer notar que esta idea de osciladores es una representación matemática y algo abstracto, y no es que haya o se asuman muellecitos o algo similar en cada punto del espacio.

Un excurso sobre el término "campo"

El término "campo" se usa en la física de dos formas diferentes, que pueden llevar a confusión. Una acepción, la más fundamental, es la que hemos usado aquí. El universo contiene sólo unos cuantos campos, tantos como tipos de partículas elementales. Para un determinado tipo de partícula elemental (por ejemplo el electrón) todas las partículas de tal tipo (todos los electrones del universo) con sus respectivas antipartículas (todos los positrones del universo) son excitaciones de un único campo. Lo mismo por ejemplo con todos los fotones del universo, creados por el campo electromagnético (o campo del fotón). Esta es la noción fundamental de campo en la teoría cuántica de campos.

Esta es la forma de hablar cuando se habla de campos en la teoría cuántica de campos. Luego, hay otra noción de campo, cuando se dice por ejemplo que un electrón crea un campo electrostático alrededor de él. Hay que tener en cuenta que son dos formas diferentes de hablar. ¿Cómo se reduce esta segunda a la primera, que es la fundamental? Denotemos por *campo* a la noción fundamental dada por la teoría cuántica de campos y por **campo** a la idea procedente de la física clásica, de que una partícula crea un campo a su alrededor. Por un lado, el *campo* electromagnético (el campo del fotón) crea o puede crear fotones como excitaciones de si mismo. Por otro lado el electrón (excitación a su vez del *campo* del electrón) crea un **campo** alrededor de él y que este ejerce una fuerza sobre cualquier carga que esté dentro de él.

Pues bien, cuando un electrón crea una fuerza sobre una carga cualquiera existen excitaciones del *campo* electromagnético que se propagan por el espacio en forma de partículas virtuales. La acción de estas partículas virtuales da lugar al **campo** del electrón. El **campo** y su geometría (simetría esférica, etc.) es consecuencia de las partículas virtuales y excitaciones del *campo*. Estas partículas virtuales son creadas sólo en caso de interacciones; el *campo* del electrón actúa como fuentes y sumideros para el *campo* electromagnético.


Esto también es un campo, pero ni es un *campo* ni un **campo**.

La radiación de Hawking

Volvamos con la noción del vacío de un campo (*campo*). El acuerdo sobre las propiedades del vacío entre sistemas inerciales, se pierde en caso de sistemas acelerados y también en caso de sistemas sometidos a la gravitación. Si yo estoy en un sistema inercial y tú estás siendo acelerado, y estamos tú y yo midiendo un determinado campo en una región del espacio, yo diré que el campo está vacío, pero tú podrás decir que no, que hay partículas en él. Este es uno de los resultados menos intuitivos de la teoría cuántica de campos y muestra que la noción de partícula es algo relativo, mientras que lo fundamental es la idea de campo. La transformación de ondas planas sinusoidales frente a aceleraciones es muy diferente a frente a transformaciones inerciales. Aquí no ocurre que todas las frecuencias se desplacen un valor constante, sino que ciertas frecuencias se aglomeran y dan lugar a una distribución diferente. Para una aceleración uniforme se puede mostrar que lo que se obtiene es una distribución térmica en las ondas planas mencionadas.

Al igual que una aceleración uniforme crea una distribución térmica de oscilaciones (denominada radiación de Unruh), por el principio de equivalencia un campo gravitatorio uniforme crea una distribución térmica de oscilaciones. Este resultado se puede extrapolar para otro tipo de campos gravitatorios, como el creado por un agujero negro. Lo que ocurre es que el observador estacionario el en campo (y por tanto acelerado) ve un vacío diferente al observador en caída hacia el agujero negro (y por tanto inercial). El vacío cerca de un agujero negro puede considerarse en cierta medida como en libre hacia él (por argumentos que me voy a ahorrar aquí) por lo que el observador acelerado (estacionario en el infinito) verá una distribución térmica de partículas saliendo de allí.

En definitiva, el orígen de esta distribución no tiene nada que ver con partículas virtuales, sino con la naturaleza del campo en su estado fundamental. Las partículas virtuales sólo aparecen cuando hay dos o más campos en interacción. La radiación de Hawking, de existir, se daría también si en el universo hubiese un único campo. Si hay más de un campo, como en la realidad por ejemplo electromagético, gluones, quarks, electrón/positrón, etc. la radiación de Hawking significará que de cada tipo de campo aparecerá una radiación térmica hacia el infinito. Naturalmente tal fenómeno es más notable para fotones debido a la fuerza de la interacción electromagnética, pero, en principio, cualquier campo sufre el mismo efecto.

Epílogo

Hemos visto que la densidad de energía del vacío viene dada por las contribuciones de las energías de los estados fundamentales de los osciladores armónicos con los que se modela un campo. Esto considerando un campo o cada campo aislado. Habiendo dos campos en su estado fundamental - sin partículas - puede que estos estén en interacción. Dado que no hay partículas que se propagan por el espacio-tiempo hasta detectores no hay líneas con extremos abiertos, sino sólo burbujas de partículas virtuales:


La figura muestra arriba una burbuja para el caso del electromagnetismo y abajo para otro tipo de interacción.

Hemos visto que si tenemos un sólo campo en el universo hay radiación de Hawking, térmica, de los agujeros negros. Si tenemos varios y los consideramos todos libres, habrá igualmente radiación de Hawking, térmica, de cada campo por separado. Pero, ¿y si tenemos varios campos en interacción? ¿Habrá alguna corrección a la radiación de Hawking, térmica, de cada campo por separado? Desconozco la respuesta, y parece una pregunta digna de ser estudiada.