La materia oscura y su densidad media
La idea de densidad media de un componennte del universo está justificada debido al principio cosmológico, que nos indica que la distribución de cualquier componente en el universo (como materia o radiación) es homogenea e isótropa a muy grandes escalas. Con ello tiene sentido definir una densidad media que es válida en cada punto siempre y cuando estemos considerando el universo a grandes escalas. Para la determinación de la densidad media de cualquier componente del universo se hace uso del concepto de densidad crítica, que es la densidad que necesitaría nuestro universo para que su geometría espacial fuese plana. Esto significa que los ángulos de un triángulo (de dimensiones cosmológicas) sumarían 180°. Si la densidad media total es menor que la crítica, la geometría es abierta y los ángulos sumarían menos de 180° y si la densidad media total es mayor que la crítica la geometría es cerrada y los ángulos sumarían más de 180°. La densidad de cualquier componente se describe en relación a la crítica y se denonta con la letra

Curvatura del universo según su densidad igual, mayor o menor que la crítica
La materia oscura es esencialmente materia no observada directamente, pero de la que se tienen indicios de su existencia debido a observaciones indirectas astrofísicas y cosmológicas. La naturaleza de esa materia es desconocida y básicamente se clasifica en dos grupos. La mayor parte se cree que es materia no-bariónica (no compuesta por quarks formando protones y neutrones), y que no interactúa electromagnéticamente sino solo gravitatoriamente y frente a la interacción débil, y otra menor parte es materia bariónica como objetos compactos o nubes de gas. De la parte no-bariónica hay razones para pensar que han de ser partículas exóticas deconocidas y que no pueden ser neutrinos. De la parte bariónica hay razones para pensar que ha de tratarse de nubes intergaláticas y que no pueden ser objetos compactos. Esto lo veremos a continuación.
Las curvas de rotación de las galaxias espirales
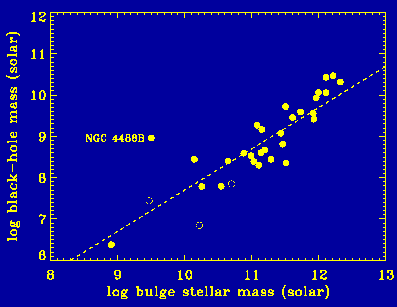
Primero, como he mencionado, el orígen del problema es meramente astrofísico y está en las curvas de rotación de las galaxias espirales. La velocidad de las estrellas en el disco galáctico es mucho mayor de lo que la gravitación que ejerce la materia visible galaxia sobre ellas debería permitir. Deberían salirse por la tangente. Para ajustar velocidad y gravitación hace falta hasta unas diez veces más materia que la observada en cada galaxia. Para la determinación de la cantidad total de materia oscura hace falta recurrir no obstante a métodos algo más generales. Aquí hay dos fuentes principales de información. Primera, los cúmulos galácticos y, segunda, la combinación de las observaciones del fondo cósmico de microondas con las supernovas Ia. Empecemos com los cúmulos.

Velocidades de rotación observadas y predichas según la materia visible
La materia oscura y los cúmulos galácticos
Análogamente al caso de las estrellas dentro de las galaxias, la dinámica de las galaxias dentro de los cúmulos sugiere la existencia de mucha más masa que la que se observa,
Otra prueba de la existencia de materia oscura es el efecto de lente gravitacional (desviación de la luz en un espacio-tiempo curvo) que los cúmulos ejercen sobre fuentes de luz situadas detrás de ellos, que es dependiente de la masa del cúmulo. Observando lentes gravitacionales se puede inferir sobre la masa de los cúmulos galácticos y se comprueba de hecho que la masa necesaria es hasta diez veces la observada. Por último, otra prueba más en relación con los cúmulos es el efecto Sunyaev-Zeldovich: Los fotones del fondo cósmico de microondas interactúan con los electrones libres del gas intracumular (scattering de Compton inverso) y obtienen energía de ellos saliéndose de la curva del cuerpo negro que conforman. El resultado es una anisotropía (un “fleco” en el mapa debido a fotones más calientes) visible en los mapas del fondo cósmico (WMAP, etc.). La potencia de este “fleco” depende de la temperatura y densidad de los electrones, que a su vez, dado un modelo de equilibrio hidrostático, proporciona información sobre el perfil de densidad del cúmulo y su masa.

Efecto de lente gravitacional producido por un cúmulo galáctico
Todo en uno hay que decir que las diferentes pruebas experimentales mencionadas, que son las más importantes, no acaban de converger con toda precisión necesaria todavía. No obstante, indican una densidad de materia de aproximadamente
La formación de estructuras de gran escala y la materia oscura
El universo empieza siendo homogeneo e isótropo una fracción de segundo tras su inicio. Esto es debido a un mecanismo denominado inflación que ocurre una fracción de segundo después del big-bang y que debido a la expansión extrema aplana cualquier condición inicial inhomogenea, dando lugar a homogeneidad. La inflación, además, proporciona un mecanismo físico por el cual las fluctuaciones cuánticas durante ese periodo del universo se convierten en perturbaciones reales de densidad energética o inhomogeneidades. Está claro que algo así es necesario, ya que de otra forma en un universo totalmente homogeneo nunca se podrían formar estructuras de materia por colapso gravitatorio.
Tras la inflación, la materia no-bariónica empieza a colapsar gravitatoriamente en las inhomogeneidades producidas por la inflación. Al no interactuar electromagnéticamente y no perder energía por disipación en procesos radiativos, su colapso es en principio más lento que el de la materia bariónica. La materia bariónica también empieza a colapsar, no obstante, su colapso se ve impedido por su fuerte interacción con los fotones que hay en el universo, cuya energía y su momento lineal son suficientes como para impedirlo. Este tira y afloja entre gravitación y presión de la radiación hace que el plasma de bariones y electrones existente antes de la recombinación sufra oscilaciones que son de gran importancia en el análisis del fondo.
Esa situación se da hasta la recombinación, unos 300.000 años tras el big-bang, cuando los fotones pierden suficiente energía debido a la expansión del espacio como para que se forme hidrógeno neutro (los fotones ya no pueden disociar el hidrógeno que se forma). La radiación y los bariones se desacoplan, quedando un fondo de radiación (que da lugar al fondo de microondas) y unos bariones libres en colapso, colapsando sobre las inhomogeneidades de materia no-bariónica. Debido a la casi homogeneidad perfecta el fondo de radiación está a una temperatura determinada y se comporta como la emisión de un cuerpo negro. El colapso de los bariones, disipativo, es a partir de entonces muy rápido. Los grumos de materia bariónica encuentran pozos de potencial preexistentes de materia oscura y empiezan a colapsar gravitacionalmente sobre ellos. Esto asumiendo que los grumos mencionados tienen una masa suficiente para ello, que resulta ser de unas
Si los pozos de potencial de materia oscura no preexistiesen al colapso bariónico en la época de la recombinación, entonces no habría suficiente tiempo hasta hoy para que el grueso de masas iniciales de
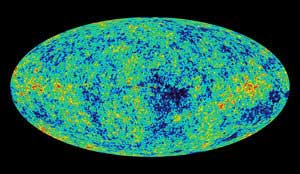
Anisotropías del fondo cósmico de microondas
Es decir, las regiones de mayor densidad y temperatura dan lugar a fotones menos energéticos y vice versa. Esto significa que en el mapa del fondo las regiones azules corresponden con zonas de sobredensidades y las regiones rojas con densidades menores. Las oscilaciones mencionadas son además visibles en el fondo debido a este efecto y son identificables debido a su escala angular, muy característica. Adicionalmente, las anisotropías que se ven en el mapa contienen además de ese otros efectos secundarios como el Sunyaev-Zeldovich mencionado anteriormente. Pero son las anisotropías correspondientes con las oscilaciones las que permiten determinar la curvatura del espacio. La idea es que la escala angular de las oscilaciones es una característica dependiente del modelo y si las observamos hoy, 13 mil millones de años después, somos capaces de indentificar si su imagen está distorsionada por una posible curvatura del espacio. Las observaciones del fondo indican que este no es el caso. Esto significa que la densidad total está cercana a la crítica.
No obstante, la utilidad de estas observaciones va más allá de todo esto. El cuadro que he descrito aquí del modelo cosmológico estándar con el colapso de materia oscura no-bariónica y consiguiente colapso de bariones, se ve verificado en las mediciones de las anisitropías. Sin embargo, hay que notar que existen cierta degeneración en los parámetros, es decir, existen otros modelos que también encajan con los datos y sólo con observaciones adicionales se pueden eliminar ambigüidades.
La energía oscura y la materia oscura
A esto vamos ahora. El fondo cósmico nos dice que la densidad total es igual a la crítica ¿Significa esto que la densidad de la materia es igual a la crítica,
La energía oscura tiene una densidad positiva, al igual que la materia, pero ejerce una presión negativa, al contrario que la radiación o la materia relativista. Esta presión hace que el la expansión del espacio acelere. Ambas se relacionan en una ecuación de estado

Expansión acelerada debido a la energía oscura según los datos de las supernovas Ia
La nucleosíntesis del big-bang y la materia oscura
Por otro lado, el modelo cosmológico estándar proporciona una medida muy exácta de la densidad media de bariones. Ésta queda delimitada por la nucleosíntesis del big-bang, un proceso que genera núcleos de dos o más nucleones determinando abundancias relativas de ellos. Ocurre en una época temprana del universo (un segundo después del big-bang), cuando los fotones pierden suficiénte energía como para no poder disociar más los núcleos. La teoría nos indica que la densidad media de bariones respecto de la crítica es
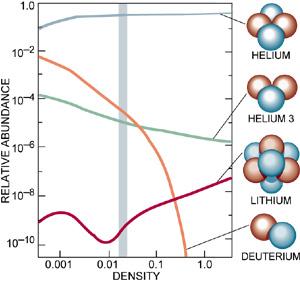
Abundancias relativas según la nucleosíntesis del big-bang (línea gris)
La materia oscura bariónica
No obstante, existe una gran parte de
La materia oscura no-bariónica
Nos queda por ver cuál es la naturaleza de la materia oscura no-bariónica. En el modelo cosmológico estándar la formación de estructuras es por acreción de menores en mayores (“bottom-up”). Tras la recombinación, primero se froman estructuras bariónicas de una masa de unas 10.000 masas solares que colapsan sobre los potenciales de materia oscura no-bariónica y más tarde se van uniendo hasta formar galaxias y cúmulos galácticos. Para ello es necesario que existan fluctuaciones de densidad suficientemente pequeñas que permitan las formación de las mencionadas estructuras después de la recombinación. La teoría predice que si la materia oscura no-bariónica fuesen neutrinos, las fluctuaciones de densidad serían eliminadas por su velocidad relativista en la época de la recombinación.
Esto es debido a un fenómeno de amortiguamiento. En este contexto significa la disminución de la profundidad del pozo gravitatorio de una perturbación. Para materia bariónica el amortiguamiento se da debido a la presión. Para partículas que no colisionan (al no interactuar electromagnéticamente) como la materia no-bariónica, el amortiguamiento se da debido a la capacidad de las partículas de escapar al pozo de potencial debido a su velocidad. Para partículas no-relativistas de materia no-bariónica fría, la distancia media de difusión es grande: su velocidad es grande de forma que se distribuyen de forma homogenea hasta una distancia determinada. A mayores distancias la gravitación es dominante y liga a las partículas en la perturbación. Esto es el amortiguamiento por difusión libre, el cual hace que las perturbaciones sólo pueden existir a partir de un determinado tamaño. La formación de estructuras bottom-up de acuerdo con las observaciones (espectro de potencia y correlación de galaxias) significa por tanto que la materia oscura no puede ser relativista o caliente.
La materia oscura no-bariónica es por tanto tal que durante la recombinación su velocidad es no-relativista. A este tipo de materia oscura se la denomina fría. Además, la masa estimada de los neutrinos no parece ser suficiente para que éstos proporcionen el total de la materia oscura no-bariónica. No se conocen partículas así, por lo que la conclusión es que todas las observaciones nos están poniendo de manifiesto los efectos de una partícula desconocida, cuya existencia está más allá del modelo estándar de partículas.
Resumen
Resumiendo. Debido a ciertos fenómenos gravitatorios se asume la existencia de materia oscura bariónica y materia oscura no-bariónica en el universo. La materia oscura bariónica ya no lo es realmente, porque poco a poco se ha ido identificandola y se sabe que existe en grandes nubes de gas intergaláctico. La materia oscura no-bariónica compone el grueso de la materia del universo y es fría, por lo que se asume que está formada por partículas que sólo interactúan a través de la gravitación y la fuerza nuclear débil, que, además, son masivas y no relativistas en la época de la recombinación. A estas partículas se las denomina genéricamente WIMPs, weakly interacting massive particles. Existen experimentos para su detección directa que se básan en la detección por choques contra núcleos atómicos que esperan tener resultados en los próximos años.

Composición del universo