Para entender la polarización del fondo conviene primero recordar el proceso similar de polarización por reflexión sobre una superficie:

De forma heurística, la luz sin polarizar incidente que entra por la izquierda interactúa con los electrones de la superficie y los excita induciendo vibraciones en ellos. Estas vibraciones llevan luego a la reemisión de luz como luz reflejada. Puesto que los electrones vibran más fácilmente en el plano de la superficie, la luz reflejada está básicamente polarizada perpendicularmente al plano de la interacción.
La interacción de Thomson da lugar a un proceso similar de polarización en el fondo. Consideremos la radiación viniendo desde la izquierda hacia un electrón. El estado de tal fotón puede expresarse como superposición y combinación lineal de las dos polarizaciones que presenta, que representan dos estados básicos:
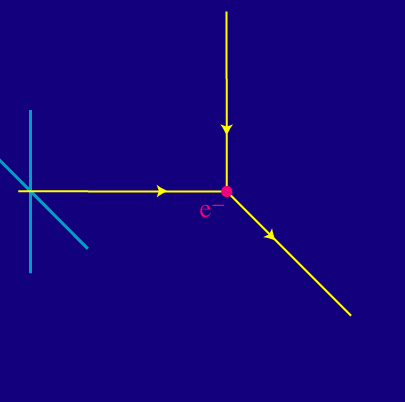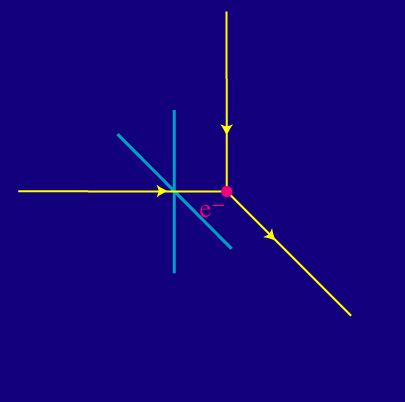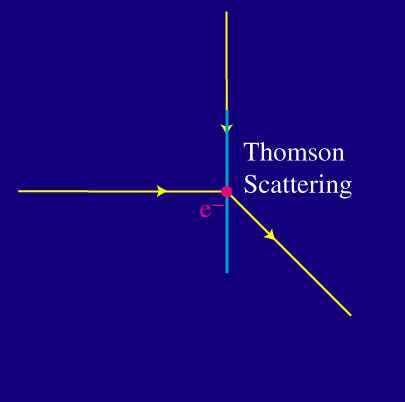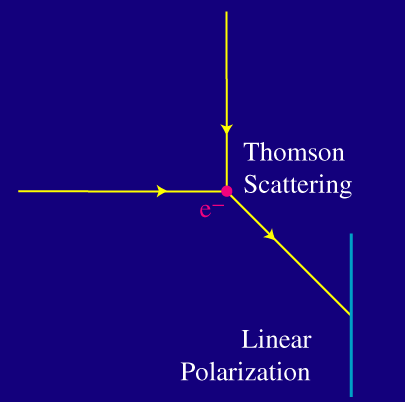
Como la luz no se puede polarizar a lo largo de su dirección del movimiento, sólo uno de los dos estados básicos de polarización consigue interactuar. Por supuesto no hay nada particularmente especial sobre la luz que viene desde la izquierda. Consideremos ahora luz que proviene tanto de la izquierda como de arriba:
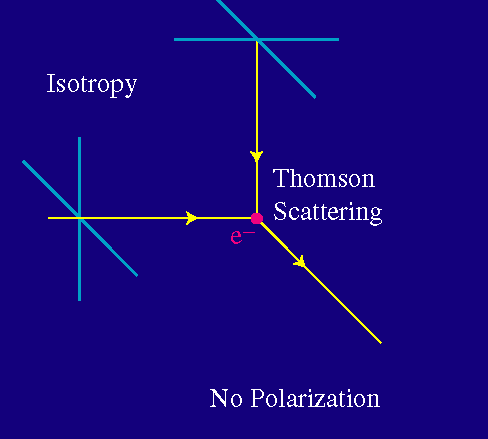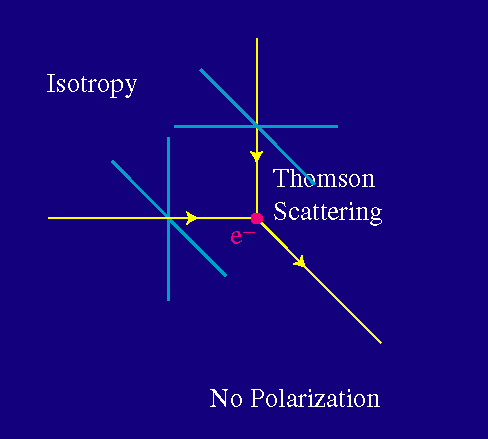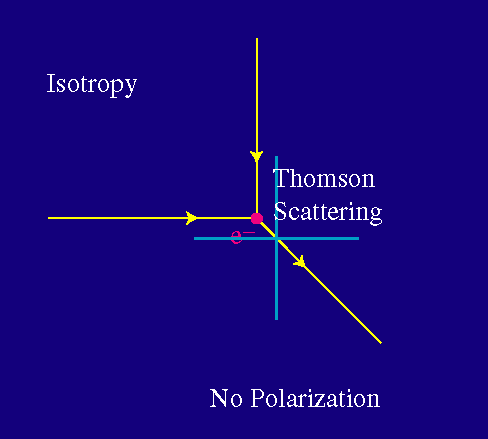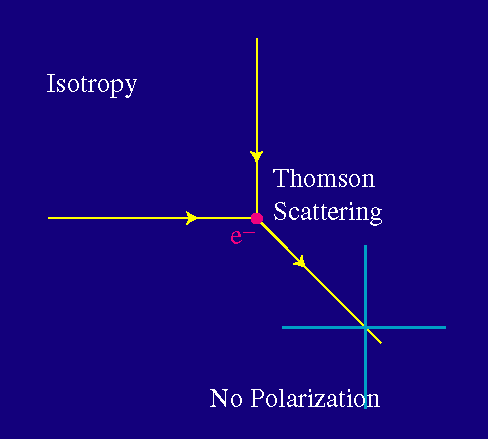
Uno de los dos estados básicos de polarización consigue interactuar en ambos casos. Pero ahora, la radiación saliente posee ambos estados de polarización. Si la radiación de la izquierda y la de arriba tienen igual intensidad, el resultado es que no hay polarización de la luz saliente.
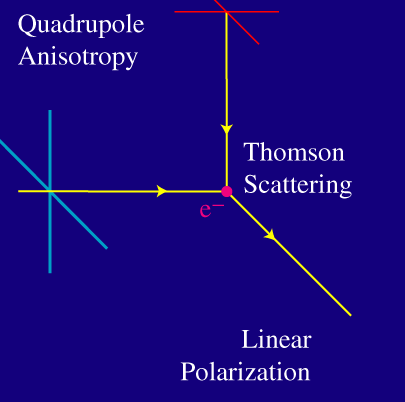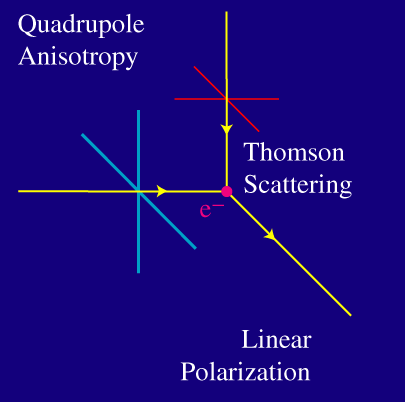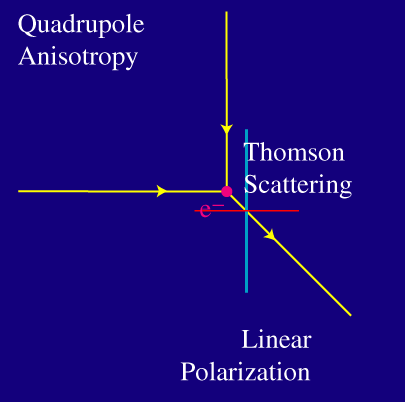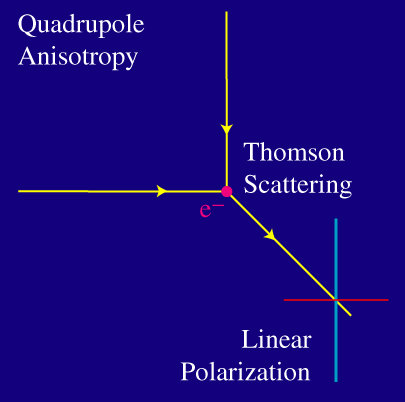
Únicamente si la intensidad de la radiación es distinta en la izquierda y arriba, o, en general si la intensidad varía en 90 grados - o, equivalentemente, la distribución corresponde con un cuadrupolo - el resultado neto es de polarización.
Una vez entendida la polarización (gracias Wayne) nos debemos preguntar si existe una distribución de radiación correspondiente a un cuadrupolo en el fondo y qué es el significado de esto.
Para entender cómo se analizan las anisotropías partamos de la observación que el cielo es una esfera con centro en nosotros, sobre la cual cualquier punto puede ser localizado por medio de dos ángulos θ, φ. El fondo cósmico de microondas cubre todo el cielo y presenta zonas en las que existen unas diferencias de temperatura (anisotropías) observadas de más o menos 0.0001 grados sobre o bajo la temperatura media del fondo de unos 2.73° K.
Esto se suele denotar así: Θ(θ, φ) = ΔT(θ, φ) / T, que viene a ser una determinada posición del cielo (dada por θ, φ) en la cual hay una diferencia de temperatura ΔT sobre la media T. Para algunas anisotropías la diferencia de temperatura es algo mayor, para otras algo menor. La desviación en un punto determinado puede extenderse en sus inmediaciones sólo un poco y decaer al valor medio o extenderse en un área mayor y luego decaer. Resumiendo, Θ(θ, φ) es una función continua con valores en toda la esfera celeste y se la denomina mapa de anisotropías. Al igual que se puede descomponer cualquier onda o señal eléctronica en sus componentes o modos de Fourier, este mapa se puede expresar en función de una de una suma de armónicos esféricos.
Θ(θ, φ) = Σlm alm Ylm(θ, φ)
Los armónicos esféricos Ylm (polinimios de Legendre) son funciones analíticas que se determinan con dos números l y m. El valor de l da la posición del armónico (l = 0, monopolo, l = 1 dipolo, l = 2 cuadrupolo, l = 3 octopolo, etc.) y m, que va desde -l hasta +l en enteros, proporciona en sus valores distintos de cero el número de lóbulos separados por nodos. Por ejemplo, para el dipolo l = 1, se tiene m = -1, 0, +1, por lo que el dipolo tiene dos lóbulos, es decir, es como un "ying-yang". Por tanto, en la suma anterior, l va desde cero hasta infinito y m desde -l hasta +l para cada l. Los armónicos de l muy grandes corresponden con funciones con gran cantidad de nodos y lóbulos. Existe una relación entre multipolo y escala angular del lóbulo dada por θ = 180° / l.
Para cada uno de estos lóbulos y armónicos hay que determinar un coeficiente, alm, que nos dará la potencia del lóbulo. Por ejemplo si un alm es cero significa que ese lóbulo de un determinado armónico no contribuye a la serie. Pero ocurre que, en general, se quiere obtener información que sea independiente de las características particulares de nuestro cielo en concreto (visto desde la tierra), es decir, los alm. Se quiere información que sea válida para cualquier observador del fondo cósmico de microondas. Esta es la información física que se ha de extraer del fondo y para esto se requieren métodos estadísticos para calcular valores medios de cantidades relevantes.
En definitiva, en principio puede existir un cuadrupolo ya que existen anisotropías. No obstante, el cuadrupolo podría ser cero, pero las observaciones nos indican que no lo es. El modelo estándar de cosmología con la inflación postula un orígen físico muy determinado del cuadrupolo. Está relacionado con perturbaciones tanto escalares, como vectoriales y tensoriales de la métrica cosmológica debidas a inhomogeneidades. Estos tipos de perturbaciones producen signaturas diferentes en la polarización. Sin entrar en detalles, que el interesado puede consultar aquí, el "E-mode", ya medido por el WMAP, tiene su orígen en las perturbaciones escalares, mientras que el "B-mode", cuya detección se espera posible con el Planck, tiene su orígen en las perturbaciones vectoriales y tensoriales, en concreto podría ser debido a un fondo de ondas gravitacionales.


No hay comentarios:
Publicar un comentario