skip to main |
skip to sidebar
Pues eso, hasta finales de julio. Tras las vacaciones nos esperan los prometidos artículos sobre la cosmología cuántica de lazos, la cosmología de cuerdas y la relación de ambas con el programa científico del satélite Planck...

Para explicar la polarización voy a traducir, aunque de forma muy libre, esta página de Wayne Hu, que se dedica a la docencia e investigación del fondo cósmico de microondas y tiene unos gráficos excelentes. Así que nada mejor que él y sus gráficos para explicárnoslo.
Para entender la polarización del fondo conviene primero recordar el proceso similar de polarización por reflexión sobre una superficie:

De forma heurística, la luz sin polarizar incidente que entra por la izquierda interactúa con los electrones de la superficie y los excita induciendo vibraciones en ellos. Estas vibraciones llevan luego a la reemisión de luz como luz reflejada. Puesto que los electrones vibran más fácilmente en el plano de la superficie, la luz reflejada está básicamente polarizada perpendicularmente al plano de la interacción.
La interacción de Thomson da lugar a un proceso similar de polarización en el fondo. Consideremos la radiación viniendo desde la izquierda hacia un electrón. El estado de tal fotón puede expresarse como superposición y combinación lineal de las dos polarizaciones que presenta, que representan dos estados básicos:
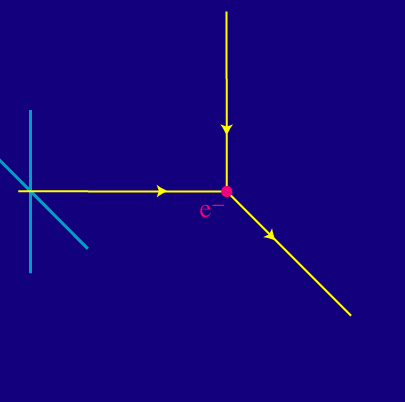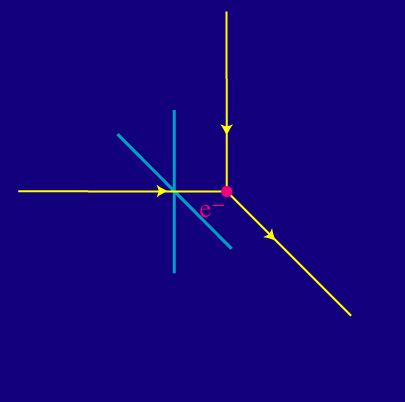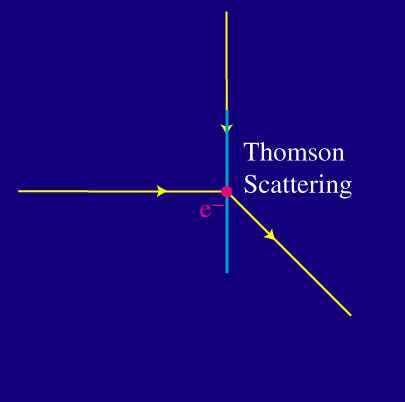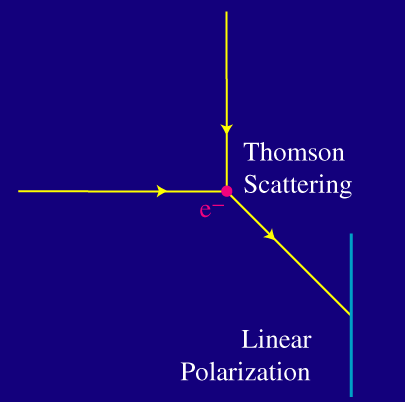
Como la luz no se puede polarizar a lo largo de su dirección del movimiento, sólo uno de los dos estados básicos de polarización consigue interactuar. Por supuesto no hay nada particularmente especial sobre la luz que viene desde la izquierda. Consideremos ahora luz que proviene tanto de la izquierda como de arriba:
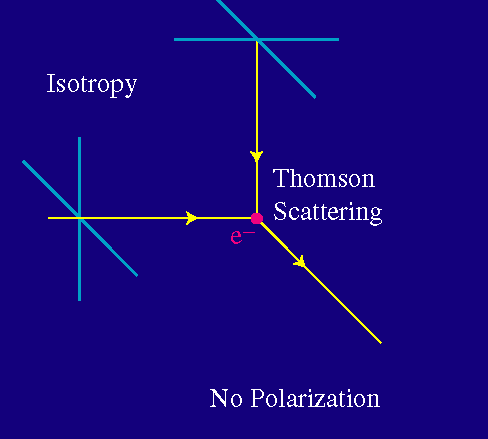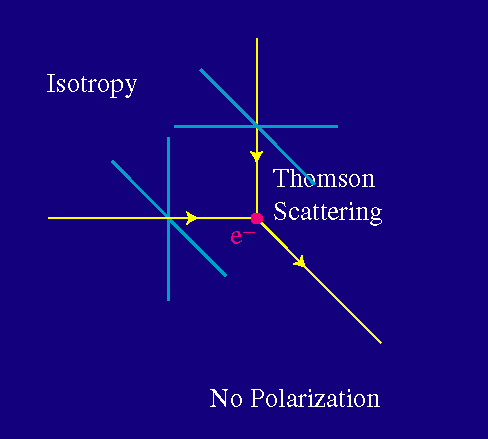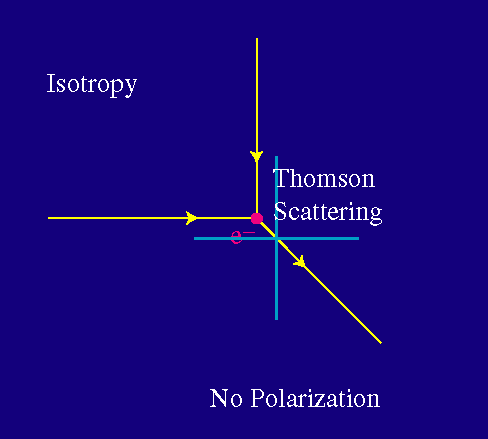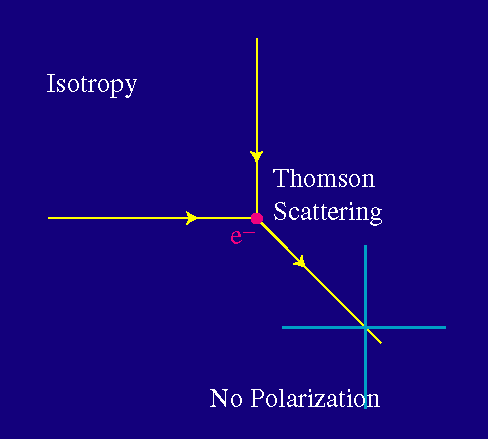
Uno de los dos estados básicos de polarización consigue interactuar en ambos casos. Pero ahora, la radiación saliente posee ambos estados de polarización. Si la radiación de la izquierda y la de arriba tienen igual intensidad, el resultado es que no hay polarización de la luz saliente.
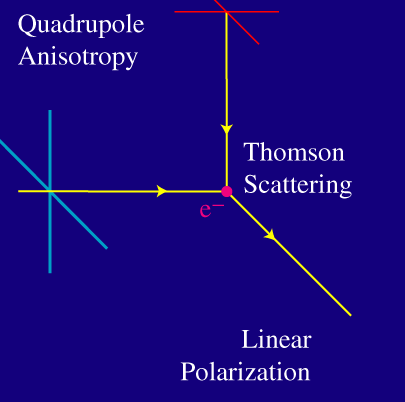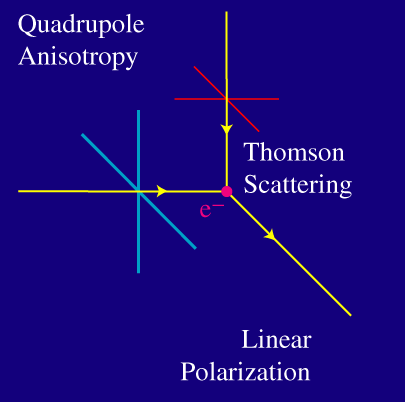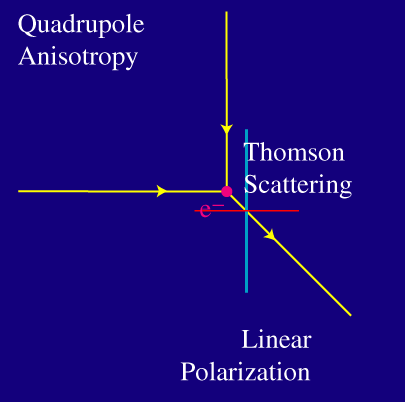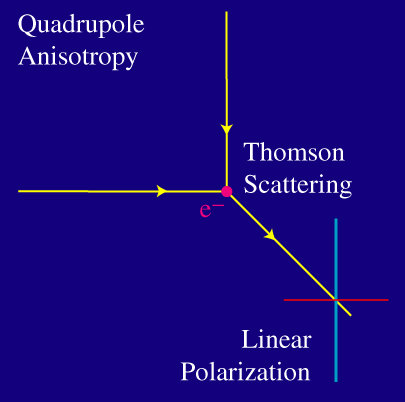
Únicamente si la intensidad de la radiación es distinta en la izquierda y arriba, o, en general si la intensidad varía en 90 grados - o, equivalentemente, la distribución corresponde con un cuadrupolo - el resultado neto es de polarización.
Una vez entendida la polarización (gracias Wayne) nos debemos preguntar si existe una distribución de radiación correspondiente a un cuadrupolo en el fondo y qué es el significado de esto.
Para entender cómo se analizan las anisotropías partamos de la observación que el cielo es una esfera con centro en nosotros, sobre la cual cualquier punto puede ser localizado por medio de dos ángulos θ, φ. El fondo cósmico de microondas cubre todo el cielo y presenta zonas en las que existen unas diferencias de temperatura (anisotropías) observadas de más o menos 0.0001 grados sobre o bajo la temperatura media del fondo de unos 2.73° K.
Esto se suele denotar así: Θ(θ, φ) = ΔT(θ, φ) / T, que viene a ser una determinada posición del cielo (dada por θ, φ) en la cual hay una diferencia de temperatura ΔT sobre la media T. Para algunas anisotropías la diferencia de temperatura es algo mayor, para otras algo menor. La desviación en un punto determinado puede extenderse en sus inmediaciones sólo un poco y decaer al valor medio o extenderse en un área mayor y luego decaer. Resumiendo, Θ(θ, φ) es una función continua con valores en toda la esfera celeste y se la denomina mapa de anisotropías. Al igual que se puede descomponer cualquier onda o señal eléctronica en sus componentes o modos de Fourier, este mapa se puede expresar en función de una de una suma de armónicos esféricos.
Θ(θ, φ) = Σlm alm Ylm(θ, φ)
Los armónicos esféricos Ylm (polinimios de Legendre) son funciones analíticas que se determinan con dos números l y m. El valor de l da la posición del armónico (l = 0, monopolo, l = 1 dipolo, l = 2 cuadrupolo, l = 3 octopolo, etc.) y m, que va desde -l hasta +l en enteros, proporciona en sus valores distintos de cero el número de lóbulos separados por nodos. Por ejemplo, para el dipolo l = 1, se tiene m = -1, 0, +1, por lo que el dipolo tiene dos lóbulos, es decir, es como un "ying-yang". Por tanto, en la suma anterior, l va desde cero hasta infinito y m desde -l hasta +l para cada l. Los armónicos de l muy grandes corresponden con funciones con gran cantidad de nodos y lóbulos. Existe una relación entre multipolo y escala angular del lóbulo dada por θ = 180° / l.
Para cada uno de estos lóbulos y armónicos hay que determinar un coeficiente, alm, que nos dará la potencia del lóbulo. Por ejemplo si un alm es cero significa que ese lóbulo de un determinado armónico no contribuye a la serie. Pero ocurre que, en general, se quiere obtener información que sea independiente de las características particulares de nuestro cielo en concreto (visto desde la tierra), es decir, los alm. Se quiere información que sea válida para cualquier observador del fondo cósmico de microondas. Esta es la información física que se ha de extraer del fondo y para esto se requieren métodos estadísticos para calcular valores medios de cantidades relevantes.
En definitiva, en principio puede existir un cuadrupolo ya que existen anisotropías. No obstante, el cuadrupolo podría ser cero, pero las observaciones nos indican que no lo es. El modelo estándar de cosmología con la inflación postula un orígen físico muy determinado del cuadrupolo. Está relacionado con perturbaciones tanto escalares, como vectoriales y tensoriales de la métrica cosmológica debidas a inhomogeneidades. Estos tipos de perturbaciones producen signaturas diferentes en la polarización. Sin entrar en detalles, que el interesado puede consultar aquí, el "E-mode", ya medido por el WMAP, tiene su orígen en las perturbaciones escalares, mientras que el "B-mode", cuya detección se espera posible con el Planck, tiene su orígen en las perturbaciones vectoriales y tensoriales, en concreto podría ser debido a un fondo de ondas gravitacionales.
Según el modelo del big-bang, hubo una época en la cual el universo estuvo formado por una sopa de partículas en la cual los fotones chocaban constantemente con los electrones (en un proceso que se conoce como scattering o interacción de Thomson). Una de las hipótesis principales del modelo del big-bang es que el universo pasa por puntos en los que hay un equilibrio termodinámico, por lo menos de forma bastante aproximada. Esto permite asignar al universo entero una temperatura única en ciertos periodos de su historia.
Debido a la expansión del universo, esta sopa de partículas perdió temperatura (al aumentar adiabáticamente el volumen de un fluido, su temperatura disminuye), bajando lo suficiente como para que los electrones y los protones que deambulaban también por ahí, se unieran para formar hidrógeno neutro. Los fotones se encontraron entonces con camino libre para viajar sin interacción, ya que los electrones con los que habían estado chocando antes dejaron deambular libremente y quedadon ligados a los protones. Este periodo de la historia del universo se denomina recombinación y ocurrió unos 300.000 años después del big-bang a una temperatura de 3.000° K. La materia y la radiación quedaron disociadas (a la recombinación se la denomina también a veces desacople) y a partir de entonces seguirán caminos distintos.
Las anisotropías del fondo cósmico de microondas son desviaciones de la curva de cuerpo negro que corresponde con una temperatura de 2.73 K. Hay dos tipos de anisotropías, las primarias y las secundarias. Las primarias fueron producidas ya durante el periodo de recombinación y las secundarias se producen desde la recombinación hasta hoy. La razón anisotropías primarias es la siguiente. Por un lado, el fluido de materia y radiación oscilaba antes de la recombinación. Estas oscilaciones producían zonas de compresión y rarefacción, es decir, sobre y subdensidades en la materia bariónica. Cuando el fondo se crea estas zonas corresponden a temperaturas mayores y menores respectivamente.
Por otro lado, la materia bariónica y los fotones de la época de antes de la recombinación estaban immersos en potenciales gravitatorios formados por la materia oscura. Estos cúmulos de materia y fotones, al ser de una densidad mayor que el promedio, tenían una temperatura mayor. La materia bariónica, no obstante, no podía colapsar más aún debido a su interacción con los fotones. Cuando dejan de interactuar y los fotones quedan libres, éstos salen o caen en los pozos de potencial y para ello vencen o son ayudados por la fuerza de la gravedad. Un fotón que vence la fuerza de la gravedad ha de perder algo de energía por lo que su frecuencia ha de dismunir (desplazamiento al rojo gravitacional). Es decir, las regiones de mayor temperatura dan lugar a fotones menos energéticos y vice versa. Esto significa que en el mapa del fondo que has puesto las regiones azules corresponden con zonas de sobredensidades (sobredensidades de 1/10.000 sobre la media) y las regiones rojas con densidades menores.

Resumiendo, las anisotropías primarias dan información sobre la cantidad y tamaño de los pozos de potencial, es decir, de las inhomogeneidades en el universo temprano. La cantidad y tamaño de las inhomogeneidades es algo muy dependiente de la fase inicial de expansión del universo. La inflación es una fase de expansión acelerada que ocurre tras el big-bang y se cree que genera homogeneidad "estirando" inhomogeneidades hasta fuera de los límites del universo observable. Durante este proceso se produce a su vez un espectro determinado de inhomogeneidades, como resultado de fluctuaciones cuánticas del vacío.
Concrétamente, la inflación con expansión exponencial, en la cual el factor de escala varía como a = exp(K t), crea un espectro de inhomogeneidades que es invariante de escala. El factor de escala da una medida de la diferencia de distancias entre dos tiempos cosmológicos. La idea intuitiva de un espectro invariante de escala es que ni las perturbaciones o pozos de potencial de pequeña escala ni las de gran escala han de dominar.
Entrando un poco en detalles, expresando los tamaños de las inhomogeneidades de acuerdo con un número de onda k, esto significa que la contribución a la varianza de las amplitudes P(k) de las inhomogeneidades es una función constante de k. Es decir, para una varianza (x²) de desviaciones cuadráticas medias de la densidad, que no es mas que el contraste de densidad (x²) = (δρ/ρ)², su espectro de potencial P(k) queda definido como:
(x²) = ∫ P(k) dk = ∫ k P*(k) d(ln k)
La definición de invarianza de escala exige igual potencia por intervalo logarítmico, por lo que P*(k) = 1/k (para un modelo unidimensional para simplificar). Es decir:
P(k) = const = k^{n-1}
por lo que n = 1. A n se lo conoce como índice espectral.
Dejando de lado detalles técnicos lo importante es que el espectro invariante de escala es necesario debido a criterios de estabilidad: si no queremos que el espacio-tiempo cosmológico de fondo sea dominado por perturbaciones de densidad tarde o temprano, desfigurándolo, necesitamos invarianza de escala o equivalentemente un índice espectral n = 1 o muy cercano a ese valor.
En concreto, para n >>1, las inhomogeneidades de pequeñas escalas dominarían se observarían hoy gran cantidad de agujeros negros. Para n << 1, las inhomogeneidades de gran escala dominarían y observaríamos desviaciones de la homogeneidad e isotropía a gran escala. Es decir, toda teoría que prediga desviaciones frente a la invarianza de escala ha de explicar también cuándo ocurren estas y en qué grado para acomodarse a la observación actual de un universo homogeneo e isótropo.
El caso es que existe una relación estrecha entre el parámetro de estado y la desviación respecto de la invarianza de escala. El parámetro de estado relaciona presión y densidad de un fluido perfécto, que son los únicos componentes posibles en los modelos del universo que cumplen homogeneidad e isotropía. Concrétamente, p = w ρ. Una expansión exponencial perfecta requiere de un parámetro de estado exáctamente igual a w = -1 y esto a su vez implica un índice espectral n = 1. Para casos de expansión superinflacionaria (más rápida que la expansión exponencial) el parámetro de estado es w < -1 y el índice espectral n > 1. Para casos de expansión en términos de potencias (más lenta que la expansión exponencial) el parámetro de estado es w > -1 y el índice espectral n < 1.
Con esto estamos equipados para entender el efecto de las teorías de cosmología cuántica sobre el espectro de potencia del mapa de las anisotropías del fondo. Antes de ello veremos sin embargo la polarización.
Este es el primero de una serie de artículos sobre la gravitación cuántica y el satélite Planck.
El satélite Planck proporcionará un mapa detallado del fondo cósmico de microondas que probablemente permita verificar o refutar algunos modelos o clases de modelos de cosmología cuántica. Especialmente la cosmología cuántica de lazos, que predice desviaciones características de la invarianza de escala en el espectro de anisotropías, o la cosmología cuántica de cuerdas, que predice una determinada pauta en la polarización debida a un fondo de ondas gravitacionales.
La ciencia de los modelos, en concreto la gravitación cuántica de lazos y la gravitación cuántica de cuerdas, así como sus predicciones las veremos en las siguientes entradas. Esta entrada está dedicada al satélite Planck en general.
La misión Planck
El satélite Planck de la ESA proporcionará un mapa del fondo cósmico de microondas (CMB) con una precisión sin precedentes, con una resolución por debajo de 10 minutos de arco y menos de una millonésima de grado de temperatura. Proporcionará también un mapa robusto y preciso de la polarización del CMB.
El lanzamiento del Planck está previsto para el mayo de 2008 y el satélite será puesto en órbita en el punto L2, al igual que fue el WMAP. Esto permitirá medir las fluctuaciones de la temperatura lejos de las influencias térmicas de la tierra.
Los objetivos científicos principales
El Planck medirá el mapa de la temperatura así como el mapa del polarizacion. Especialmente, la medida exacta de la polarización será uno de los logros más notables del Planck.
El espectro de anisotropías del CMB fue medido ya con la alta precisión por WMAP, el cual midió también la polarización con un grado aceptable de exactitud. Sin embargo, hay razones científicas importantes que requieren una medición de la polarización con un grado más alto de exactitud. Especialmente la diferenciación entre los modos tensoriales y escalares de la polarización, cosa que debería aclarar la naturaleza de la inflación. Véase esta entrada de mi blog. Con ello, las pruebas para algunos modelos de cosmología cuántica podrían estar a la vuelta de la esquina.
No vamos a dejar este tema tan interesante en estas simples palabras confusas. La relación entre el mapa de anisotropías de temperatura y el mapa de polarización con la física de los modelos de la gravitación cuántica de lazos y la gravitación cuántica de cuerdas lo veremos con detalle en las siguientes entradas en este blog. Explicaré primero qué es el mapa de anisotropías y el de polarización y luego veremos cómo esos modelos pueden predecir sus características. Nótese lo fabuloso del asunto: extrapolando física conocida hasta límites insospechados formulamos unos modelos sobre el orígen del universo observable y luego pretendemos poder probarlos ya dentro de unos años. Una aventura increible y difícil, pero heróica como la que más.
Volvamos a las medidas que realizará el Planck. Por otro lado, un mapa de la polarización y un espectro de anisotropías más preciso deben servir como comprobaciones de consistencia sobre las estimaciones actuales de parámetros cosmológicos. Además, tercero, la polarización debe clarificar el proceso del reionización después de la edad oscura, así como la cantidad y el espectro de los objetos compactos bariónicos (que miden los efectos de lentes gravitacionales en la polarización del fondo). Éstas son todas las metas que no eran posibles con WMAP.
El análisis de los datos
Un mapa de la alta precisión del CMB requerirá de una cantidad formidable de datos que tendrán que ser transmitidos a la tierra. Para simplificar el volumen de este proceso el Planck comparará los datos con una predicción de los mapas realizada en base a las últimas mediciones más precisas del WMAP y enviará únicamente las diferencias entre lo observado y la predicción. En la tierra y con esta diferencia se reconstruirá el mapa completo.
Sin embargo, el proceso y el analisis de los datos de telemetría es una tarea extremadamente compleja. En la misión Planck esta tarea se ha dividido en cuatro niveles.
- El nivel 1, que abarca el análisis de los datos que contienen la supervisión de los datos de los instrumentos y del satélite así como los datos científicos.
- El nivel 2, del proceso de la información científicas para la creación y la calibración de los mapas del cielo de los diversos instrumentos en diferentes frecuencias, importante para eliminar emisiones de ruidos.
- El nivel 3, del proceso de datos del nivel anterior para la creación de los mapas del cielo, tales como el espectro de energía de CMB, interpretable de forma científica. Una vez más, una parte fundamental en el nivel 3 es la identificación de los ruidos debidos a emisiones de primero plano por fuentes galáticas como emisión del sincrotrón, emisión térmica, etc. Todos estos fenómenos fueron tratados y analizados ya con mucho detalle por el WMAP.
- El nivel 4, para la preparación de la información para las publicaciones científicas.
El satélite y los instrumentos
El satélite en si mismo se compone de dos partes fundamentales, el payload module (módulo de carga útil) y el service module (módulo de servicio):

Puedes ver un modelo 3D aquí.
El payload module contiene un telescopio y dos detectores así como los sistemas criogénicos necesarios para mantener los detectores a bajas temperaturas. El telescopio enfoca la radiación electromágnetica en los detectores. El primer detector es un instrumento de baja frecuencia radiométrico (Low Frequency Instrument, LFI). Segundo un instrumento es bolométrico de alta frecuencia (High Frequency Instrument, HFI). Ambos instrumentos se mantienen respectivamente a 20 K y 100 mK y medirán la radiación entre 30 GHz y 100 GHz para el LFI y entre 100 GHz y cerca de 850 GHz para el HFI.
El diseño de la carga fue realizado de tal manera que el Planck y el Herschel puedan ser lanzados juntos. Esto requiere de un adaptador que se colocará en el Ariane.
Información detallada se sobre los instrumentos se puede encontrar aquí.
El módulo de servicio contiene todo lo necesario para hacer que el satélite funcione de forma apropiada, como telecomando, telemetría y preprocesado de datos en el subsistema de datos, producción y almacenamiento de energía de la luz solar, control térmico, avionica, etc.
Referencias
Consideremos un modelo simplificado de universo clásico, concrétamente el modelo de de-Sitter. El modelo de de-Sitter resulta cuando se considera un espacio-tiempo completamente vacío pero con una constante cosmológica. Este modelo es homogeneo e isótropo no solo en el espacio, sino también en el tiempo. Se trata de un modelo de en el cual cualquier punto del espacio-tiempo es igual a todos los demás.
En las soluciones de Friedmann-Robertson-Walker con singularidad inicial sólo los puntos de una sección espacial son todos iguales, mientras que los puntos en secciones espaciales diferentes no tienen por qué ser iguales, es decir, no tienen por qué tener características iguales de densidad, curvatura, etc. En el modelo de-Sitter, sin embargo, todos los puntos son iguales. Esto significa que el modelo no presenta una singularidad inicial.

La desconocida naturaleza de la constante cosmológica, que produce la expansión un modelo de-Sitter
La métrica del espacio-tiempo de de-Sitter es ds² = - dt² - a² dl² con a = 1/H cosh(Ht) siendo H el parámetro de Hubble que es constante en este modelo. Para t = 0 el factor de escala tiene un valor mínimo con a = 1/H. El modelo clásico de-Sitter impide la existencia de un universo que se inicia en t = 0 comportándose ya como uno de-Sitter, ya que el espacio-tiempo está perféctamente definido en -oo < t < +oo.

La evolución del factor de escala en el modelo de de-Sitter
Lo sorprendente es que la cosmología cuántica canónica en el minisuperespacio (véase entrada anterior) hace posible aparición de un universo que empieza a comportarse en t = 0 como uno de-Sitter, haciéndolo aparecer en el régimen clásico t > 0. El mecanismo involucrado es el efecto túnel que tiene lugar desde un estado sin correspondencia clásica alguna, a través de un potencial efectivo, hasta el estado clásico de de-Sitter.
Para verlo, partamos de la primera ecuación de Friedmann con una constante cosmológica, para un espacio cerrado k = 1:
a'²/ a² + 1 / a² - L = 0
Tomando el momento conjugado del factor de escala p = a a':
p²/a + a - a³ L = 0
Sustituyendo según la prescripción del método de cuantización de Dirac a -> a, p -> - i h d/da, a operadores que actúan sobre una función de onda del universo F(a), se tiene:
[h² d²/da² - V(a)] F(a) = 0
Esta es la ecuación de Wheeler-deWitt para este modelo concreto. Es similar a la ecuación de Schrödinger para una partícula en un potencial V, que describe su comportamiento cuántico. Para resolver esta ecuación se procede igual que en el caso de una partícula puntual sometida a un potencial haciendo uso de la aproximación semiclásica de WKB (Wentzel-Kramers-Brillouin). Las soluciones se separan en dos tipos, las clásicas oscilatorias y las de efecto túnel exponencialmente decrecientes. Es decir, la partícula o bien se mueve como una onda ahí donde no está el potencial, o bien pasa a través del potencial debido al efecto túnel.

El efecto túnel a través del potencial efectivo V(a)
Para obtener las soluciones concretas hace falta imponer condiciones iniciales, tal y como he mencionado en la entrada anterior de este blog.
Una de las diferencias esenciales de la ecuación de Wheeler-deWitt para este modelo concreto y la ecuación de Schrödinger es que la segunda describe una evolución respecto de un parámetro temporal t externo al sistema. Sin embargo, en la relatividad general tal parámetro no existe y uno ha de decidirse por la elección de un parámetro interno, de entre muchos posibles. En muchos de los modelos de cosmología cuántica, como el modelo tratado aquí, ese parámetro interno es el factor de escala.
No obstante, hay una diferencia fundamental en imponer condiciones iniciales para un tiempo externo o imponerlas para el factor de escala en a = 0 como parámetro interno. Dado que un modelo cerrado puede colapsar en un big-crunch, la imposición de condiciones iniciales en a = 0 corresponde con dos valores diferentes del tiempo clásico. Esto parece ir en contra del determinismo de las trayectorias clásicas del universo así como de la flecha del tiempo.
Este tipo de problema requiere de una diferenciación y clara interpretación de las condiciones iniciales para la función de onda del universo y sus trayectorias clásicas. A veces el problema se suele dejar de lado ya que la cosmología cuántica pretende describir primero solo el orígen del universo que queda claramente en nuestro pasado. Pero en definitiva esto es un ejemplo de algo fascinante: si tomamos totalmente en serio los modelos de cosmología cuántica y también gravitación cuántica, las consecuencias para nuestra comprensión de la realidad han de ser radicales.
I have never believed that reality could turn out to be fixed by an unimaginative initial condition.
Esta cita de Bryce deWitt nos muestra uno de los más serios problemas de los modelos de cosmología cuántica basados en la cuantización canónica de la relatividad general. Intentemos entenderla.
La cosmología cuántica es la rama de la cosmología que describe los primeros instantes del universo, durante los cuales el universo se considera como un objeto de comportamiento cuántico. Para formular una cosmología cuántica es necesaria una teoría de gravedad cuántica que unifique la relatividad general con la mecánica cuántica.

Bryce deWitt
La relatividad general predice su propia incapacidad de describir estados como los agujeros negros o el big-bang, denominados singularidades, en los que la curvatura del espacio-tiempo se hace infinita. La relatividad general resulta ser la herramienta inadecuada para describir la evolución del universo en una época ya anterior al tiempo de Planck. Antes del tiempo de Planck las altas energías y las distancias pequeñas involucradas hacen que los efectos cuánticos del campo gravitatorio dejen de ser despreciables y se conviertan en ingrediente necesario para cualquier descripción consistente y completa de la física del universo.
La gravedad cuántica canónica es una teoría de gravedad cuántica que pretende cuantizar de forma usual la relatividad general, como en otras teorías cuánticas por medio de un exitoso procedimiento de cuantización ideado por Dirac a principios del siglo veinte. Para definir la teoría se separa el espacio-tiempo M en espacio y tiempo M = S x t y se define como variable dinámica fundamental la métrica hij con i, j = 1, 2,3 de las hipersuperficies S. Este formalismo es equivalente a las ecuaciones de Einstein que toman como variable fundamental la métrica del espacio-tiempo guv con u, v = 0, 1, 2, 3.
Para los modelos cosmológicos de cosmología cuántica canónica la métrica hij queda reducida en sus grados de libertad debido al principio cosmológico que impone homogeneidad e isotropía en las hipersuperficies S, convirtiéndo hij en la parte espacial de una métrica de Friedmann-Robertson-Walker, y, con ello, dando lugar a un único grado de libertad o variable dinámica, el factor de escala "a". El espacio de métricas espaciales reducidas por el principio cosmológico se denomina minisuperespacio.
La prescripción de cuantización de Dirac consiste, al igual que en la mecánica cuánitica no-relativista, en promover la variable dinámica y su momento conjugado a operadores que actúan en un espacio de Hilbert, a -> a, p -> - i h d/da. Estos operadores actúan sobre un funcional de métricas F(hij), que se conoce como función de onda del universo, al igual que en la mecánica cuántica no-relativista los operadores actúan sobre una función de onda.
La substitución de estas variables por operadores en la primera ecuación clásica de Friedmann (convenientemente reescrita), la cual describe la dinámica del factor de escala "a" y con ello la expansión del universo, da lugar a lo que se conoce como ecuación de Wheeler-deWitt, que describe por tanto la evolución del universo en sus inicios (dejando de lado sutilezas como el hecho que la primera ecuación de Friedmann sea en realidad una ligadura y no tanto una ecuación evolutiva). Para los modelos más sencillos la ecuación de Wheeler-deWitt es formalmente equivalente a la ecuación de movimiento de una partícula puntual sometida a un potencial. Al igual que en el caso de la partícula puntual, para resolver esta ecuación se procede por medio de aproximaciones semiclásicas.
Lo que viene a cuento aquí y ahora es que para obtener las soluciones concretas hay que imponer condiciones de contorno o iniciales. ¿Cuáles han de ser estas condiciones de contorno? ¿Por qué deberíamos decirle al universo cómo empezar a ser o a expandir? Nihil est sine ratione. Cualquier elección injustificada convierte las condiciones en indemostrables y no ducibles, elevándolas al mismo estatus conceptual que los mismos principios de la teoría. Diferentes elecciones para las condiciones de contorno del universo inicial han dado lugar a los modelos de cosmología cuántica más famosos hasta la fecha, como el de Hartle-Hawking ("no-boundary proposal") o el de Vilenkin ("tunneling proposal").
Existe sin embargo otra opción imaginable: no imponer condiciones iniciales. Bryce deWitt soñó con una teoría cuya consistencia interna evitase imponer condiciones de contorno o iniciales para el universo. Es decir, una teoría en la que la necesidad de consistencia interna diese lugar a una solución única. Esto no fue posible en los modelos de cosmología cuántica canónica, pero resulta ser posible con algunos modelos actuales basados en teorías matemáticamente más refinadas como la cosmología cuántica de lazos basada en la gravedad cuántica de lazos.

¿Condiciones iniciales del espacio-tiempo cuántico o sólo la ilusión de una ciencia todavía infantil?
En cualquier caso, esto es un ejemplo de cómo ideas fundamentadas guían una ciencia (la cosmología cuántica) de la cuál no sabemos casi nada. Ideas que se mantienen pese a la insistencia de las matemáticas en no ajustarse a ellas y que, tarde o temprano, son retomadas por nuevos modelos. Es lo que distingue la buena física del mero juego matemático con las ecuaciones. En otro artículo hablaré sobre la relevancia de las condiciones iniciales en la cosmología cuántica de lazos.
Un artículo de Bryce-deWitt sobre memorias de juventud, creacionismo y actividad científica y su sentido:
http://www.aip.org/pt/vol-58/iss-1/p32.html
Nihil est sine ratione, nada existe sin razón, desde la hoja de un árbol hasta la distribución de galaxias en el universo. Es más, no es que nada exista sin razón, sino que nada de lo que existe es trivial.
Este es un hecho que en el mundo moderno nos pasa desapercibido con demasiada frecuencia. Cualquier cosa está relacionada de forma delicada y sutil con el resto del universo, lo grande con lo pequeño, lo lejano con lo cercano, y existe con dignidad y presencia constante.

La distribución de materia en el universo y una hoja tienen más en común de lo que parece a simple vista
Según Lee Smolin (The case for background independence), para la ciencia física el principio de razón suficiente tiene un valor algo menos poético pero también efectivo. Impone que ha de ser posible dar una justificación racional para cualquier atributo u objeto matemático de entre un conjunto de objetos o atributos posibles en una teoría, siempre y cuando esos objetos del conjunto correspondan con diferentes realidades medibles. Esto es, el principio de la indentidad de los indiscirnibles es condición necesaria para que el principio de razón suficiente sea aplicable.
Por ejemplo, no existe experimento para responder la pregunta de por qué el universo no empezó cinco minutos antes o cinco después. Ambas situaciones son físicamente la misma en el marco de nuestra teoría actual, ya que lo observable o medible es su edad actual. Ahora bien, una teoría que fija sin justificación la geometría del espacio-tiempo viola este principio. Igualmente, lo viola una teoría que fija sin justificación la masa del electrón. Y también lo viola una teoría que fija sin justificación la cantidad de dimensiones espaciales.
Todo esto son parámetros o atributos que de ser distintos tendrían un efecto muy claro y medible en nuestra realidad. Estos atributos u objetos han de obtenerse o bien de forma dinámica de la teoría o bien por consistencia matemática frente a los principios fundamentales de la teoría. Por ejemplo, la geometría del espacio-tiempo es de esperar que se obtenga de forma dinámica (esto es lo que usualmente se entiende hoy por "background independence" o independencia del fondo), tal y como nos indica la relatividad general, o la cantidad de dimensiones podría derivarse de condiciones de consistencia con objetos fundamentales como cuerdas, etc.

Gottfried Leibniz y Lee Smolin
El papel enlazado arriba "The case for background independence" de Lee Smolin tiene un claro trasfondo técnico, pero también es interesante desde un punto de vista más general, de filosofía de la ciencia, y por tanto, recomendable para el interesado en estos temas.








